سالاد میوهها©
تعداد بردها: 134296
برای برنده شدن : چهار قطعه رنگی سمت راست صفحه را به سمت چپ صفحه منتقل کنید تا فقط میوههایی که در بالای سوال دیده میشوند، در صفحه قابل مشاهده باشند و بقیه میوهها پوشانده شوند.
روش بازی : روی یکی از قطعههای سمت راست صفحه کلیک کنید تا انتخاب شود. بعد از انتخاب یک قطعه، شما میتوانید آن را با نگه داشتن کلید سمت چپ ماوس جابجا کنید و سپس برای قرینه کردن یا دوران آن، بر روی کلیدهای پایین صفحه کلیک کنید. وقتی که مطمئن هستید که پاسخ سوال را پیدا کردهاید، روی دکمه «ارسال جواب» کلیک کنید تا پاسخ شما بررسی شود.
توجه : شما میتوانید از کلیدهای میانبر در صفحه کلید هم استفاده کنید (روی دکمه «نمایش کلیدهای کنترل» کلیک کنید تا آنها را نمایش دهد). اگر فکر میکنید انیمیشن تمرکز شما را بر هم میزند، بر روی دکمه «انیمیشن را خاموش کن» کلیک کنید.
| کلید W یا کلید جهت بالا : قطعه انتخابی را به سمت بالا حرکت میدهد. | کلید S یا کلید جهت پایین : قطعه انتخابی را به سمت پایین حرکت میدهد. |
| کلید A یا کلید جهت چپ : قطعه انتخابی را به سمت چپ حرکت میدهد. | کلید D یا کلید جهت راست :قطعه انتخابی را به سمت راست حرکت میدهد. |
| Q :قطعه انتخابی را در خلاف جهت عقربههای ساعت میچرخاند. | E :قطعه انتخابی را در جهت عقربههای ساعت میچرخاند. |
| F :قطعه انتخابی را قرینه میکند. | R :صفحه را دوباره میچیند و بازی از ابتدا آغاز میشود. |
| ورودارسال جواب | T :میتوانید بین قطعهها بچرخید. |



- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
اگر شما قبل از اینکه این نکتهها را ببینید، با تلاش زیاد توانستهاید پاسخ سوال را پیدا کنید، به شما تبریک میگوییم. شما به مطالعه این بخش نیاز ندارید.
-
در این قسمت، منظور از «بررسی یک قطعه» این است که شما یک قطعه را روی یک قسمت از صفحه بگذارید و آن را در همه جهتهای ممکن بچرخانید یا قرینه کنید. این کار را ادامه دهید و بررسی کنید که آیا میوههایی که قابل مشاهده هستند، بخشی از پاسخ هستند یا خیر؟
- نکته ۱ : قسمتهایی را پیدا کنید که یک قطعه مشخص میتواند در آنجا قرار بگیرد. برای این کار میتوانید یک قطعه را در نظر گرفته و در هر قسمت از صفحه، بررسی کنید.
- نکته ۲ : قطعههایی را پیدا کنید که میتوانند در یک قسمت مشخص قرار بگیرند. میتوان با انتخاب یک قسمت و امتحان کردن هر قطعه در این قسمت، آن را بررسی کرد.
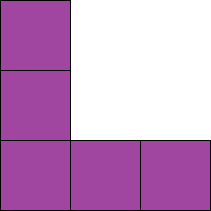
- نکته ۳ : تعداد جاهای خالی که باید قابل مشاهده باشند را تعیین کنید. در ره حالت از قرار دادن 4 قطعه بر روی صفحه، تعداد مربعهایی که قابل مشاهده خواهند بود برابر با مجموع جاهای خالی در 4 قطعه است. در این 4 قطعه ۳ + ۳ + ۳ + ۴ = ۱۳ جای خالی وجود دارد. برای پیدا کردن تعداد مربعهای خالی قابل مشاهده، تعداد میوههایی که باید قابل مشاهده باشند را از ۱۳ کم کنید.
- نکته ۴ : تعداد هر نوع میوه که در سوال وجود دارد را بشمارید. اگر یک میوه در سوال اصلا ظاهر نشده باشد، به این معنی است که هر میوه از آن نوع، باید پوشانده شود. شما باید تعداد هر نوع میوه که در صفحه ظاهر شده است را بشمارید. این به شما کمک میکند که تعداد میوههای مشابه که باید باقی بمانند را تعیین کنید.
- نکته ۵ : کار را با تلاش برای حدس زدن اینکه قطعه بنفش کجا باید قرار بگیرد شروع کنید. چون قطعه بنفش، تنها قطعهای است که مرکز آن باز است، حدس زدن اینکه باید در کدام قسمت قرار بگیرد، راحتتر است زیرا خانه میانی آن قسمت همیشه قابل مشاهده است. یک ایده خوب این است که قطعه سبز، آخرین قطعهای باشد که بررسی میکنیم. برای آن هشت دلیل داریم که در زیر بیان شده است. اگر صبر کنید و این قطعه را در آخرین مرحله بررسی کنید، این کار در زمان شما صرفهجویی خواهد کرد.
- نکته ۶ : از یک نکته استفاده کنید تا امکان استفاده از یک نکته دیگر فراهم شود. ممکن است یک نکته در پیدا کردن جای مناسب برای یک قطعه مفید نباشد اما ممکن است به شما کمک کند تا تعداد میوههایی که برای قطعههای دیگر باقی مانده است را کاهش دهد. یک مثال میتواند به این صورت باشد که فرض کنید در آخر کار، باید یک سیب قابل نمایش باقی بماند و یک قطعه مشخص داریم که همیشه یک سیب را قابل نمایش باقی میگذارد و آن را نمیپوشاند. با دانستن این موشوع، متوجه میشویم که سایر قطعهها باید تمام سیبها را بپوشانند و باعث میشود که ادامه راه حل سادهتر شده و بتوان سایر قطعهها را در جای درست قرار دارد. این مشابه بازی سودوکو است که ممکن است با استفاده از قاعده مشخصی نتوان محل یک عدد را پیدا کرد اما انتخابهای مناسب را محدود میکند بطوریکه یک قاعده دیگر بتواند جواب مناسب را پیدا کند.
- نکته 7 : فقط قطعه سبز را قرینه کنید. همانطور که در پایین گفته شده است، همه قطعهها بجز قطعه سبز دارای تقارن آیینهای هستند. بنابر این، نباید وقت خودتان را با قرینه کردن این سه قطعه هدر بدهید و فقط باید دورانهای مختلف آنها را بررسی کنید.
-
مثالهای زیر، نشان میدهند که نکتههای بخش بالا چگونه به شما کمک میکنند تا پاسخ همه معماها را پیدا کنید.
- قبل از هر چیز، این سوال از ما میخواهد که فقط 6 موز قابل مشاهده باقی بمانند و بقیه میوه ها پوشانده شوند. از نکته ۴ استفاده میکنیم، میتوانیم ببینیم که روی صفحه در مجموع فقط 6 موز وجود دارد و میخواهیم که همه آنها قابل مشاهده باشند. همچنین میدانیم که همه میوههای دیگر باید پوشانده شوند.
- در مرحله بعد، از نکته ۵ استفاده میکنیم، میبینیم که یک موز در مرکز قسمت بالا-راست صفحه وجود دارد. این به ما میگوید که فقط قطعه بنفش باید در این قسمت اینجا قرار بگیرد چون تنها قطعهای است که مرکز صفحه را نمیپوشاند. قطعه بنفش را در اینجا قرار میدهیم و آن را میچرخانیم تا اینکه سایر میوهها قابل مشاهده نباشند.
- اکنون میتوانیم به قسمت پایین-چپ صفحه نگاه کنیم. هیچ موزی در اینجا وجود ندارد، یعنی تمام میوههای این قسمت باید با یک قطعه پوشانده شوند. از نکته ۲ استفاده میکنیم و از بین ۳ قطعه باقیمانده، میتوانیم ببینیم که قطعه سبز تنها قطعهای است که همه این میوهها را میپوشاند.
- اکنون از نکته ۱ روی هر یک از دو قطعه باقیمانده استفاده میکنیم. با قطعه آبی شروع کرده و میبینیم که آن را باید روی قسمت پایین-راست صفحه قرار دهیم چون قطعه آبی بعضی از موزهای قسمت بالا-چپ را میپوشاند. در نهایت میتوانیم قطعه صورتی را در آخرین قسمت باقیمانده قرار دهیم و آن را بچرخانیم تا هر سه موز قابل مشاهده باشند.
- بیایید با نکته ۵ شروع کنیم تا تعیین کنیم قطعه بنفش کجا باید قرار بگیرد. چون در مرکز قسمت بالا-راست یک موز و در مرکز قسمت پایین-چپ یک پرتقال وجود دارد، قطعه بنفش نمیتواند در هیچیک از این دو قسمت قرار بگیرد. در مرحله بعد، اگر از نکته ۱ استفاده کنیم، میتوانیم بررسی کنیم که قطعه بنفش در قسمت بالا-چپ یا قسمت پایین-راست صفحه باید قرار بگیرد. از نکته ۴ استفاده میکنیم، میبینیم که همیشه یک سیب وجود دارد که قابل مشاهده باقی میماند. یعنی اینکه ما میتوانیم یک سیب از میوههایی که باید قابل مشاهده باشند را حذف کنیم که سوال را سادهتر میکند.
- حالا میتوانیم از نکته ۱ استفاده کنیم و ابتدا با قطعه صورتی شروع میکنیم. اکنون میدانیم که هیچ سیبی نباید قابل مشاهده باشد. پس تنها جایی که این قطعه میتواند قرار بگیرد، در قسمت بالا -راست است.
- در مرحله بعد، قطعه آبی را بررسی میکنیم. از نکته ۱ دوباره استفاده میکنیم. تنها جایی که این قطعه میتواند در آن قرار بگیرد، قسمت پایین-چپ است چون تمام موزها و پرتقالها را می پوشاند. اکنون، میبینیم که هر دو گیلاس قابل مشاهده هستند و بنابر این، میتوانیم گیلاسها را نادیده بگیریم.
- اکنون، باید جای دو قطعه باقیمانده را تعیین کنیم به طوری که هر سه انگور باقیمانده قابل مشاهده باشند. از نکته ۱ استفاده میکنیم، میتوانیم با قطعه سبز شروع کنیم و ببینیم که میتواند در قسمت پایین-راست صفحه قرار بگیرد. سرانجام، میبینیم که قطعه بنفش باید در قسمت بالا-چپ قرار بگیرد و معما را حل کردهایم.
-
اکنون که شما اطلاعات بیشتری در باره بازی و راه حلهای آن دارید، بیایید یک معمای ساده را حل کنیم. بر روی کلید زیر کلیک کنید تا سوال را ببینید.
 قبل از اینکه پاسخ معما را ببینید، لطفا خودتان تلاش کنید و ببینید چقدر طول میکشد تا پاسخ را پیدا کنید.
قبل از اینکه پاسخ معما را ببینید، لطفا خودتان تلاش کنید و ببینید چقدر طول میکشد تا پاسخ را پیدا کنید.
-
اکنون، سوالی را در نظر میگیریم که شامل انواع بیشتری از میوهها است. روی کلیدزیر کلیک کنید تا سوال را نشان دهد.
- معمای سالاد میوهها وقتی سختتر میشود که انواع بیشتری از میوهها باید قابل مشاهده باشند. اگر تعداد اندکی از میوهها وجود داشته باشد، مثل اینکه اگر شما فقط به دنبال موزها و انگورها بگردید، شما فقط باید حالتهایی را پیدا کنید که قطعههای رنگی فقط اینها را نپوشانند. این به شما کمک میکند که تعداد انتخابهای ممکن را کاهش دهید و معما راحتتر حل شود.
- اگر انواع بیشتری از میوهها وجود داشته باشد، تعیین محل قرار گرفتن یک قطعه دشوارتر است و بنابراین، سوال سختتر میشود. پس لازم است که از نکتههای بیان شده استفاده کنیم، به ویژه وقتی که میخواهیم سوالهای سخت بیشتری را حل کنیم (مثال سخت بالا را نگاه کنید).
- مورد دیگری که معمای سالاد میوهها را سختتر میکند این است که برای پیدا شدن محل صحیح قرار گرفتن یک قطعه، آن را چند مرتبه باید جابجا کرد، قرینه کرد یا دوران داد. هر سوال، فقط یک جواب دارد یعنی اینکه برای پیدا کردن پاسخ درست باید بعضی از حرکتها حتما اجرا شوند. ترتیب اجرای این حرکتها مهم نیست و بعضی از حرکتها میتوانند با حرکتهای دیگر جابجا شوند (مثلا، سه مرتبه چرخاندن یک شکل به سمت راست برابر با یک بار چرخاندن آن به سمت چپ است). سوالی که به تعداد بیشتری از این حرکتها نیاز داشته باشد، سختتر است چون زمان بیشتری طول میکشد تا پاسخ درست پیدا شود.
-
یک قطعه میتواند انواع متفاوتی از تقارن، تقارن آینهای و یا تقارن چرخشی داشته باشد. یک قطعه متقارن آینهای است هرگاه قرینه آن مشابه چند مرتبه دوران آن باشد. یک قطعه متقارن چرخشی است هرگاه دوران 90 درجه آن مشابه خود آن قطعه باشد.
-
سه تا از قطعهها در این بازی، متقارن آینهای هستند. قطعههای صورتی و بنفش نسبت به قطر متقارن هستند و قطعه آبی، متقارن افقی است. قطعه سبز، متقارن عمودی نیست. برای این بازی، مهم نیست که محور تقارن چه باشد زیرا هر قطعه میتواند چرخانده شود.



-
هیچ یک از قطعهها در این بازی، وقتی که چرخانده شوند مشابه همان شکل قبلی نیستند. قطعههایی که دارای این نوع تقارن هستند (که در این بازی وجود ندارد) شامل یک خط راست یا شکل X هستند.

-
یک قطعه با تقارن آینهای فقط 4 حالت دارد که باید بررسی شود. بنابراین، قطعههای صورتی، آبی و بنفش هر کدام 4 حالت دارند. یک قطعه که تقارن آینهای نداشته باشد 8 حالت مختلف دارد که باید بررسی شود. چون قطعه سبز، تنها قطعهای است که متقارن نیست، تنها قطعهای هم هست که 8 حالت مختلف دارد. شما میتوانید آن را با دوران در جهت عقربههای ساعت بررسی کنید و سپس هر قطعه را قرینه کرده و آن را دو باره بچرخانید.
-
وقتی که بخواهید قطعهها را در صفحه قرار دهید، برای اولین قطعه 4 انتخاب دارید، سپس ۳ مکان دیگر برای قرار دادن قطعه دوم وجود دارد، برای قطعه سوم 2 انتخاب وجود دارد و قطعه چهارم هم باید در آخرین قسمت صفحه گذاشته شود. بنابر این، تعداد کل حالتها برای انتقال 4 قطعه رنگی به سمت چپ صفحه برابر ۴ × ۳ × ۲ × ۱ = ۲۴ است. این تعداد را میتوان به صورت n ! یا ۴ فاکتوریل بیان کرد.
سه قطعه متقارن همانطور که قبلا گفته شد، میتواند به چهار حالت چرخانده شوند. یعنی تا حالا، (۴ × ۴ × ۴) × (۴ × ۳ × ۲ × ۱) = ۱۵۳۶ حالت مختلف وجود دارد.
و بالاخره، چون قطعه سبز میتواند به 8 حالت قرار گیرد، پس 4 قطعه رنگی را به (۸ × ۴ × ۴ × ۴) × (۴ × ۳ × ۲ ×۱) = ۱۲۲۸۸ حالت مختلف، میتوان در صفحه قرار داد.
-
در مجموع، (۸ × ۸ × ۸ × ۸) × (۴ × ۳ × ۲ × ۱) = ۹۸۳۰۴ حالت مختلف برای این قطعهها وجود دارد.
-
میخواهیم تعداد کل حالتها را برای 20 قطعه متقارن و ۵ قطعه نامتقارن پیدا کنیم. به جای اینکه مثل قبل، ۲۰ تا ۴ تایی و ۵ تا ۸ تایی داشته باشیم، میتوانیم فرمول جدیدی را برای سادگی این محاسبه ارائه کنیم .
از قسمت بالا، میدانیم که تعداد حالتها برای یک قطعه نامتقارن ۴ است. ما میتوانیم ببینیم که برای n قطعه متقارن، تعداد کل انتخابها برابر 4n است.
به طور مشابه، میدانیم که تعداد حالتها برای یک قطعه نامتقارن، ۸ است و تعداد حالتهای ممکن برای m نامتقارن برابر8m است.
همانطور که قبلا بیان شد، برای پیدا کردن تعداد کل حالتهایی که قطعهها (بدون در نظر گرفتن چرخشها) میتوانند در یک صفحه قرار بگیرند، از s ! استفاده میکنیم که s تعداد قطعهها میباشد.
اگر اینها را در هم ضرب کنیم، میتوان نتیجه گرفت ۴^n × ۸^m × s! = t که't' تعداد کل جاهایی است که میتواند هر قطعه در آن قرار بگیرد
چون ۲^۲ = ۴ و ۲^۳ = ۸ ، این فرمول میتواند بهصورت زیر ساده شود
4n * 8m = (22)n * (23)m
= (22n) * (23m)
= 22n + 3m
فرمول نهایی ۲^(۲n + ۳m) × s! = t است که 'n' تعداد قطعههای متقارن، 'm' تعداد قطعههای نامتقارن، 's' تعداد کل قطعهها است که میتواند همچنین با n + m محاسبه شود و 't' تعداد مکانهایی است که برای قطعهها وجود دارد. از این فرمول استفاده کن تا تعداد مکانها را برای صفحه تعیین کنید (یک قطعه نامتقارن و ۳ قطعه متقارن وجود دارد)
اکنون، میدانیم که این فرمول درست است. میتوانیم حدس بزنیم که تعداد جاهایی که برای صفحه که در ابتدای این بخش با ۲۰ قطعه متقارن و ۵ قطعه نامتقارن توضیح داده شده است، حدس بزنیم.
22n + 3m * 25! = t
22(20) + 3(5) * 25! = t
240 + 15 * 25! = t
255 * 25! = t
5.59 x 1041 = t
(این جواب دقیق به صورت ۵۵۸۸۵۰۲۳۸۱۶۹۶۸۷۳۸۸۷۳۰۳۸۸۶۷۹۶۰۹۰۲۴۵۱۲۰۰۰۰۰۰ است یا پانصد و پنجاه دوادکلیون، هشتصد و پنجاه آندکلیون، دویست و سی هشت دکیلیون،صد و شصت و نه نانیلیون، ششصد و هشتاد و هفت اکتیلیون، سیصد و هشتاد و هشت سپتیلیون، هفتصد و سی سکتیلیون، سیصد و هشتاد و هشت کوانتیلیون، ششصد و هفتاد و نه کوادریلیون، ششصد و نه تریلیون، بیست و چهار بیلیون، پانصد و دوازده میلیون)
-
وقتی که میدانیم چگونگی پیدا کردن تعداد جاها نمیتواند به شما کمک کند تا معما را حل کنید، آن همچنان مفید است. در حالیکه این بازی را پیشرفته کردهایم، نیاز داریم که مطمئن شویم که هر سوال فقط یک پاسخ دارد. برای این موضوع، ابتدا باید همه حالتهایی ممکن را برای این صفحه پیدا کنیم. برای ذخیره کردن این جاها، از یکآرایه, که هر کدام یک اندازه مشخص دارند. از فرمول بالا استفاده میکنیم تا تعیین کنیم هر آرایه باید چه اندازهای داشته باشند.
-
چهار قطعه روی صفحه از مربعهای کوچکتر ساخته شده است. سه تا از آنها از ۶ مربع و یک قطعه دیگر از ۵ مربع ساخته شده است.
شکلی که از تعدادی از مربعهای کوچکتر ساخته شده است، یک پولیمینو نامیده میشود. اسامی مشخصی برای شکلهایی با تعداد معینی از مربعها وجود دارد هگزومینوها از شش مربع ساخته شدهاند و پنامینوها از پنج تا مربع ساخته شدهاند
بازی مشهور زیادی از پولیمینوها استفاده میکنند مانند تتریسو قطعهها و دومینوها نسخههای دیگری از بازی سودوکو وجود دارد که از پولیمینوها به جای مربعها استفاده کرده است
اطلاعات بیشتر در مورد بازیهای پولینوموها را میتوان در لینکهای زیر پیدا کرد :





برای به روز رسانی عضو شوید و یا ما را دنبال کنید: