សាលាដផ្លែឈើ©
ចំនួនសរុបនៃការឈ្នះ៖: 134296
របៀបឈ្នះ៖ ផ្លាស់ទី ខ្វាក់ ពី ក្ដារ ខាង ស្តាំ នីមួយៗ ទៅ លើ ក្តារ ខាង ឆ្វេង មួយ ដើម្បី ឲ្យ ផ្លែ ឈើ តែ មួយ គត់ ដែល អាច មើល ឃើញ ផ្គូផ្គង នឹង ផ្លែ ឈើ ដែល បាន បង្ហាញ នៅ ខាង លើ ក្ដារខៀន ។
របៀបលេង៖ ចុច លើ ខ្វាក់ នៅ លើ ក្ដារ ស្តាំ ដើម្បី ជ្រើស វា & # 160; ។ ពេល ជ្រើស អ្នក អាច ផ្លាស់ទី ខ្វាក់ ដោយ អូស វា ជាមួយ mouse ឬ អេក្រង់ ប៉ះ របស់ អ្នក ហើយ អ្នក អាច ចុច លើ ប៊ូតុង នៅ ខាង ក្រោម ក្ដារ ដើម្បី បង្វិល ឬ បង្វិល វា បាន ។ នៅពេលដែលអ្នកគិតថាអ្នកបានរកឃើញដំណោះស្រាយសូមចុច 'Submit' ដើម្បីពិនិត្យចម្លើយរបស់អ្នក។
ចំណាំ អ្នកអាចប្រើក្តារចុចបញ្ជាជំនួស (ចុច 'Display Keyboard Controls' ដើម្បីបង្ហាញវា) ។ ប្រសិន បើ អ្នក រក ឃើញ ចលនា រំខាន សូម ចុច 'Turn Animations Off'.
| គន្លឹះព្រួញ W ឬ UP: ២. រំកិល ខ្វាក់ ដែល បាន ជ្រើស ។ | គន្លឹះព្រួញ S ឬ DOWN: ២. រំកិល ខ្វាក់ ដែល បាន ជ្រើស ។ |
| គន្លឹះព្រួញ A ឬ LEFT: ២. រំកិល ខ្វាក់ ដែល បាន ជ្រើស ទៅ ខាង ឆ្វេង ។ | D ឬ RIGHT Arrow Key: ២. រំកិល ខ្វាក់ ដែល បាន ជ្រើស ទៅ ខាង ស្ដាំ ។ |
| Q: បង្វិល នាឡិកា ខ្វាក់ ដែល បាន ជ្រើស & # 160; ។ | E: បង្វិល នាឡិកា ខ្វាក់ ដែល បាន ជ្រើស & # 160; ។ |
| F: Flip the selected blind. | R: កំណត់ ឡើង វិញ នូវ ក្ដារខៀន ។ |
| បញ្ចូល៖ សូម ដាក់ ជូន ចម្លើយ របស់ អ្នក ។ | T: ជិះកង់ទៅខ្វាក់ក្រោយ។ |



- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
អ្នក ទទួល បាន ច្រើន បំផុត ពី សកម្មភាព ដោយ គិត ជា លើក ដំបូង មួយ រយៈ មុន នឹង ពង្រីក ចម្លើយ ចំពោះ សំណួរ ទាំង នោះ ។ សូមរីករាយ.
-
នៅក្នុងផ្នែកនេះ "checking a blind" សំដៅទៅលើនៅពេលដែលអ្នកដាក់មនុស្សខ្វាក់នៅកន្លែងណាមួយនៅលើក្តារនិងបង្វិល/បង្វិលវាតាមទិសទាំងអស់របស់វា។ សូម តាមដាន នូវ អ្វី ដែល អាច មើល ឃើញ រាល់ ពេល ហើយ ពិនិត្យ មើល ថា តើ ផ្លែ ឈើ ទាំង នេះ ជា ផ្នែក មួយ នៃ ដំណោះ ស្រាយ ឬ អត់ ។
- គន្លឹះ #1: ស្វែងរកផ្នែកដែលមនុស្សខ្វាក់ជាក់លាក់អាចទៅបាន។ នេះ អាច ធ្វើ បាន ដោយ ពិនិត្យ មើល ភាព ខ្វាក់ ដូច គ្នា នៅ ក្នុង ផ្នែក នីមួយ ៗ នៃ ក្ដារខៀន ។
- គន្លឹះ #2: ស្វែងរកអ្វីដែលខ្វាក់អាចទៅក្នុងផ្នែកជាក់លាក់មួយ. នេះ អាច ធ្វើ បាន ដោយ ជ្រើស រើស ផ្នែក មួយ និង ពិនិត្យ មើល ភាព ខ្វាក់ នីមួយៗ នៅ ក្នុង ផ្នែក នេះ ។
- ព័ត៌មានជំនួយ #3: កំណត់ ចំនួន ការ៉េ ទទេ ដែល បាន បង្ហាញ នៅ ក្នុង ដំណោះ ស្រាយ ។ ចំនួន សរុប នៃ ការ៉េ ដែល អាច មើល ឃើញ នៅ លើ ក្តារ នៅ ពេល ណា ក៏ បាន គឺ ស្មើ នឹង ចំនួន សរុប នៃ ' រន្ធ ' នៅ ក្នុង ខ្វាក់ នីមួយ ៗ ។ ក្នុងករណីនេះ មានរន្ធ 3 + 3 + 3 + 4 = 13 រន្ធ។ ដើម្បី រក ឃើញ ចំនួន សរុប នៃ ការ៉េ ទទេ ដែល អាច មើល ឃើញ ដក ចេញ នូវ ចំនួន ផ្លែ ឈើ ដែល ត្រូវ តែ បង្ហាញ ពី ចំនួន សរុប នៃ ការ៉េ ដែល អាច មើល ឃើញ ( 13 ) ។
- Hint #4: រាប់ចំនួនផ្លែឈើប្រភេទនីមួយៗដែលលេចឡើងនៅក្នុងសំណួរ។ ប្រសិន បើ ផ្លែ ឈើ មិន លេច ឡើង នៅ ក្នុង សំណួរ ទាល់ តែ សោះ នោះ វា មាន ន័យ ថា គ្រប់ ផ្លែ នៃ ប្រភេទ នោះ ត្រូវ តែ គ្រប ដណ្តប់ ។ អ្នក ក៏ គួរ រាប់ ចំនួន ផ្លែ ឈើ ប្រភេទ នីមួយ ៗ ដែល លេច ឡើង នៅ លើ ក្ដារខៀន ផង ដែរ ។ នេះ នឹង ជួយ ក្នុង ករណី ដែល ផ្លែ ឈើ គ្រប់ ប្រភេទ ដូច គ្នា ត្រូវ តែ ទុក ឲ្យ មើល ឃើញ ។
- គន្លឹះ #5: ចាប់ផ្តើមដោយព្យាយាមរកកន្លែងដែលភ្នែកពណ៌ស្វាយគួរតែទៅ។ ដោយសារ តែ ខ្វាក់ ពណ៌ ស្វាយ គឺ ជា មនុស្ស តែ ម្នាក់ គត់ ដែល មាន មជ្ឈមណ្ឌល របស់ វា បើក ចំហ ដោយ ស្វែង យល់ ពី កន្លែង ដែល វា អាច ទៅ លើ ក្តារ គឺ ងាយ ស្រួល ជាង នេះ ដោយសារ តែ ផ្លែ កណ្តាល នៃ ផ្នែក របស់ វា នឹង អាច មើល ឃើញ ជានិច្ច ។ វា ក៏ ជា គំនិត ល្អ មួយ ក្នុង ការ ដាក់ មនុស្ស ខ្វាក់ បៃតង ចុង ក្រោយ ផង ដែរ ។ ដោយហេតុថាមានរដ្ឋចំនួន ៨ (ដូចបានរៀបរាប់ខាងក្រោម) វាអាចនឹងសន្សំពេលវេលាខ្លះប្រសិនបើអ្នករង់ចាំដាក់មនុស្សខ្វាក់នេះរហូតដល់ចប់។
- គន្លឹះ #6: ប្រើ គន្លឹះ មួយ ដើម្បី បើក មួយ ទៀត ។ ទោះបី ជា គន្លឹះ មិន ទទួល បាន ជោគ ជ័យ ក្នុង ការ ដាក់ ខ្វាក់ ក៏ ដោយ វា អាច កាត់ បន្ថយ ចំនួន ផ្លែ ឈើ ដែល អាច បន្សល់ ទុក ដោយ មនុស្ស ខ្វាក់ ម្នាក់ ទៀត ។ ឧទាហរណ៍ មួយ នៃ រឿង នេះ គឺ ប្រសិន បើ សំណួរ តម្រូវ ឲ្យ ផ្លែ ប៉ោម មួយ អាច មើល ឃើញ ហើយ ខ្វាក់ ជាក់លាក់ តែង តែ បង្ហាញ ផ្លែ ប៉ោម មួយ ។ នេះ មាន ន័យ ថា គ្មាន មនុស្ស ខ្វាក់ ណា ផ្សេង ទៀត គួរ តែ បង្ហាញ ផ្លែ ប៉ោម ដែល ធ្វើ ឲ្យ មនុស្ស ម្នាក់ ងាយ ស្រួល ក្នុង ការ ដាក់ មនុស្ស ខ្វាក់ ផ្សេង ទៀត នោះ ទេ ។ នេះ គឺ ស្រដៀង គ្នា ទៅ នឹង ការ ប្រកួត ស៊ូដូគូ ដែល អាច មាន ច្បាប់ មួយ ចំនួន ដែល នឹង មិន ជួសជុល ការ ដាក់ លេខ មួយ ប៉ុន្តែ អាច កំណត់ ជម្រើស ដែល នៅ សល់ ដូច ជា ច្បាប់ មួយ ផ្សេង ទៀត ឥឡូវ នេះ ទទួល បាន ជោគ ជ័យ ។
- ព័ត៌មានជំនួយ #7៖ ត្រឡប់តែខ្វាក់ពណ៌បៃតងប៉ុណ្ណោះ។ ដូចដែលបានពិពណ៌នាបន្ថែមពីលើនេះ ពិការភ្នែកទាំងអស់ លើកលែងតែពណ៌បៃតងមានកញ្ចក់ស៊ីមេទ្រី។ ដូច្នេះហើយ អ្នកអាចសន្សំពេលវេលាដោយមិនព្យាយាមត្រឡប់កញ្ចក់ស៊ីមេទ្រីទាំងបីនេះវិញ។ ការព្យាយាមបង្វិលទាំងអស់គឺគ្រប់គ្រាន់ហើយ។
-
ឧទាហរណ៍ ខាង ក្រោម នេះ នឹង បង្ហាញ ថា ការ ដឹង ពី គន្លឹះ ពី ផ្នែក ខាង លើ នឹង ជួយ អ្នក ដោះស្រាយ ផ្គុំ រូប ទាំង អស់។
- ដំបូង សំណួរ នេះ ចង់ ឲ្យ យើង មាន តែ ចេក ប្រាំ មួយ ប៉ុណ្ណោះ ដែល បង្ហាញ ។ ដោយ ប្រើ Hint #4 យើង អាច មើល ឃើញ ថា មាន តែ ចេក ចំនួន ៦ ប៉ុណ្ណោះ សរុប នៅ លើ ក្ដារខៀន ហើយ យើង ដឹង ថា ចេក ទាំង អស់ នោះ ត្រូវ តែ មើល ឃើញ។ យើង ក៏ ដឹង ដែរ ថា ផ្លែ ឈើ គ្រប់ ប្រភេទ ផ្សេង ទៀត ត្រូវ តែ គ្រប ដណ្តប់ ។
- បន្ទាប់មកទៀត ដោយប្រើប្រាស់ Hint #5 យើងអាចឃើញថាមានចេកមួយនៅកណ្តាលនៃផ្នែកខាងស្តាំកំពូលនៃក្តារ។ នេះ មាន ន័យ ថា ខ្វាក់ ពណ៌ ស្វាយ ត្រូវ តែ ទៅ ទី នេះ ដោយសារ តែ វា ជា មនុស្ស ខ្វាក់ តែ ម្នាក់ គត់ ដែល បន្សល់ ទុក នូវ មជ្ឈមណ្ឌល ដែល អាច មើល ឃើញ ។ យើង អាច ដាក់ ពណ៌ ស្វាយ ខ្វាក់ នៅ ទីនេះ ហើយ បង្វិល វា ដើម្បី កុំ ឲ្យ ផ្លែ ផ្សេង ទៀត បង្ហាញ ហើយ បន្ទាប់ មក បន្ត ។
- ឥឡូវ នេះ យើង អាច មើល ផ្នែក ខាង ឆ្វេង ខាង ក្រោម នៃ ក្ដារខៀន ។ នៅ ទីនេះ គ្មាន ចេក ណា ដែល មាន ន័យ ថា ផ្លែ ឈើ គ្រប់ ប្រភេទ ក្នុង ផ្នែក នេះ ត្រូវ តែ គ្រប ដណ្តប់ ដោយ ខ្វាក់ ភ្នែក នោះ ទេ ។ ដោយ ប្រើ Hint #2 ជាមួយ នឹង អ្នក ខ្វាក់ បី ដែល នៅ សល់ យើង អាច មើល ឃើញ ថា ខ្វាក់ ពណ៌ បៃតង គឺ ជា មនុស្ស តែ ម្នាក់ គត់ ដែល គ្រប ដណ្តប់ លើ ផ្លែ ឈើ ទាំង អស់ នេះ ។
- ឥឡូវនេះយើងអាចប្រើ Hint #1 នៅលើ អ្នកទាំងពីរដែលនៅសេសសល់ដោយចាប់ផ្តើមដោយភ្នែកពណ៌ខៀវ។ បន្ទាប់ ពី ធ្វើ បែប នេះ យើង អាច មើល ឃើញ ថា វា ត្រូវ តែ ចូល ទៅ ក្នុង ផ្នែក ខាង ស្តាំ បាត ដោយសារ វា មិន អាច បង្ហាញ ចេក ទាំង បី នៅ ផ្នែក ខាង ឆ្វេង កំពូល បាន ឡើយ ។ បន្ទាប់ មក យើង ដាក់ ខ្វាក់ ពណ៌ ផ្កា ឈូក ចូល ទៅ ក្នុង ផ្នែក ចុង ក្រោយ ហើយ បង្វិល វា ដើម្បី បង្ហាញ ចេក ទាំង បី ។
- តោះចាប់ផ្តើមដោយប្រើ Hint #5 ដើម្បីកំណត់កន្លែងដែលភ្នែកពណ៌ស្វាយគួរតែទៅ។ ដោយសារ ផ្នែក ខាង ស្តាំ កំពូល មាន ចេក មួយ នៅ ចំ កណ្តាល ហើយ ផ្នែក ខាង ឆ្វេង បាត នៃ ក្ដារខៀន មាន ពណ៌ ទឹកក្រូច នៅ ចំ កណ្តាល ខ្វាក់ ពណ៌ ស្វាយ មិន អាច ចូល ទៅ ក្នុង ផ្នែក ណា មួយ ក្នុង ចំណោម ផ្នែក ទាំង ពីរ នេះ បាន ទេ ។ បន្ទាប់មកទៀត ប្រសិនបើយើងប្រើ Hint #1 យើងអាចសាកល្បងពណ៌ស្វាយខ្វាក់ក្នុងផ្នែកខាងឆ្វេងកំពូលនិងផ្នែកខាងស្តាំបាត។ ដោយ ប្រើ Hint #4 យើង អាច មើល ឃើញ ថា តែង តែ មាន ផ្លែ ប៉ោម ដែល នៅ សល់ អាច មើល ឃើញ ។ នេះមានន័យថាយើងអាចកំចាត់ផ្លែប៉ោមចេញពីផ្លែដែលចាំបាច់ត្រូវទុកឲ្យមើលឃើញ ដែលធ្វើឲ្យសំណួរសាមញ្ញ។
- ឥឡូវ យើង អាច ប្រើ Hint #1 បាន យើង នឹង ចាប់ ផ្តើម ដោយ ខ្វាក់ ពណ៌ ផ្កា ឈូក ជា មុន សិន។ ឥឡូវ នេះ ដែល យើង ដឹង ថា យើង មិន អាច បង្ហាញ ផ្លែ ប៉ោម បាន ទេ យើង ឃើញ ថា កន្លែង តែ មួយ គត់ ដែល ខ្វាក់ នេះ អាច ទៅ គឺ នៅ ក្នុង ផ្នែក ខាង ស្តាំ កំពូល ។
- បន្ទាប់ មក សូម ពិនិត្យ មើល ខ្វាក់ ពណ៌ ខៀវ ដោយ ប្រើ Hint #1 ទៀត។ កន្លែង តែ មួយ គត់ ដែល ខ្វាក់ នេះ អាច ទៅ បាន គឺ នៅ ផ្នែក ខាង ឆ្វេង បាត ដោយសារ វា បង្ហាញ ពី ចេក ឬ ពណ៌ ទឹកក្រូច នៅ ក្នុង ផ្នែក ពីរ ផ្សេង ទៀត ។ ឥឡូវ នេះ យើង អាច មើល ឃើញ ថា ទំពាំង បាយ ជូរ ទាំង ពីរ អាច មើល ឃើញ ដូច្នេះ យើង អាច លុប បំបាត់ វា ចេញ ពី សំណួរ សម្រាប់ ពេល នេះ ។
- ឥឡូវ នេះ យើង ត្រូវ ដាក់ ខ្វាក់ ពីរ ដែល នៅ សល់ ដូច ជា ទំពាំង បាយ ជូរ ទាំង បី ដែល នៅ សល់ ត្រូវ បាន ទុក ឲ្យ មើល ឃើញ ។ ដោយ ប្រើ Hint #1, យើង អាច ចាប់ ផ្តើម ដោយ ខ្វាក់ ពណ៌ បៃតង ហើយ មើល ថា វា ត្រូវ តែ ចូល ទៅ ក្នុង ផ្នែក ខាង ស្តាំ បាត ។ ជាចុងក្រោយយើងអាចដាក់ពណ៌ស្វាយត្រលប់ទៅផ្នែកខាងឆ្វេងកំពូលវិញបាន។ ហើយយើងធ្វើបាន។
-
ឥឡូវ នេះ ដែល អ្នក ដឹង បន្ថែម ទៀត អំពី ល្បែង និង យុទ្ធសាស្ត្រ មួយ ចំនួន ដើម្បី ដោះស្រាយ សំណួរ សូម ដោះស្រាយ ផ្គុំ រូប Beginner ។ ចុច ប៊ូតុង ខាង ក្រោម ដើម្បី បង្ហាញ សំណួរ & # 160; ។
-
ឥឡូវ នេះ សូម ដោះស្រាយ សំណួរ ដែល ទាក់ទង នឹង ផ្លែ ឈើ ច្រើន ជាង មួយ ប្រភេទ ។ ចុច ប៊ូតុង ខាង ក្រោម ដើម្បី បង្ហាញ សំណួរ & # 160; ។
- ផ្គុំ រូប កាន់ តែ លំបាក នៅ ពេល ដែល មាន ផ្លែ ឈើ ប្រភេទ ច្រើន ដែល ត្រូវ តែ ទុក ឲ្យ រក ឃើញ ។ ប្រសិនបើមានផ្លែឈើមួយប្រភេទតូចដូចជាអ្នកគ្រាន់តែស្វែងរកតែចេក និងទំពាំងបាយជូរប៉ុណ្ណោះ អ្នកអាចចាប់ផ្តើមដោយស្វែងយល់ពីកន្លែងដែលមនុស្សខ្វាក់ទុកតែអ្វីដែលអាចមើលឃើញទាំងនេះប៉ុណ្ណោះ។ នេះ ជួយ បន្ថយ ចំនួន កន្លែង ដាក់ ដែល អាច ធ្វើ ទៅ បាន ដូច្នេះ ការ ផ្គុំ រូប គឺ ងាយ ស្រួល ដោះស្រាយ ។
- បើ មាន ភាព ខុស គ្នា កាន់ តែ ច្រើន នោះ វា កាន់ តែ ពិបាក ក្នុង ការ កាត់ បន្ថយ កន្លែង ដែល មនុស្ស ខ្វាក់ អាច ដាក់ បាន ដូច្នេះ សំណួរ គឺ ពិបាក ជាង មុន។ នេះ ជា មូល ហេតុ ដែល វា មាន សារៈ សំខាន់ ក្នុង ការ ប្រើ គន្លឹះ ដែល បាន រាយ ខាង លើ ជា ពិសេស នៅ ពេល ព្យាយាម ដោះ ស្រាយ សំណួរ ដែល ពិបាក ជាង នេះ ( សូម មើល គំរូ ដ៏ លំបាក ខាង លើ ) ។
- រឿង មួយ ទៀត ដែល ធ្វើ ឲ្យ ការ ផ្គុំ រូប របស់ ផ្លែ ឈើ សាឡាដ ពិបាក ចិត្ត គឺ ត្រូវ ផ្លាស់ ប្តូរ បង្វិល ឬ បង្វិល ខ្វាក់ ដើម្បី ទទួល បាន ចម្លើយ ត្រឹម ត្រូវ ។ សំណួរ នីមួយៗ នៅ លើ គេហទំព័រ នេះ មាន ចម្លើយ តែ មួយ គត់ ដែល មាន ន័យ ថា ពួក គេ ទាំង អស់ គ្នា មាន សំណុំ នៃ ការ ផ្លាស់ទី ផ្ទាល់ ខ្លួន របស់ ពួក គេ ដែល ត្រូវ តែ អនុវត្ត ដើម្បី ទទួល បាន ចម្លើយ ត្រឹមត្រូវ ។ ការ ផ្លាស់ ប្តូរ ទាំង នេះ មិន ចាំបាច់ ត្រូវ ធ្វើ តាម លំដាប់ ជាក់លាក់ ណា មួយ ឡើយ ហើយ ការ ផ្លាស់ ប្តូរ មួយ ចំនួន អាច ត្រូវ បាន ជំនួស ដោយ អ្នក ផ្សេង ទៀត ( ឧ. ការ បង្វិល រូប រាង បី ដង ទៅ ខាង ស្តាំ គឺ ដូច គ្នា នឹង ការ បង្វិល វា ម្តង ទៅ ឆ្វេង ) ។ សំណួរ ដែល មាន សំណុំ នៃ ការ ផ្លាស់ ប្តូរ ធំ ជាង នេះ គឺ កាន់ តែ លំបាក ដោយសារ វា នឹង ចំណាយ ពេល យូរ ដើម្បី ស្វែង រក ចម្លើយ ត្រឹម ត្រូវ ។
-
ខ្វាក់ អាច មាន ប្រភេទ ផ្សេង គ្នា នៃ ស៊ីមេទ្រី, កញ្ចក់ ស៊ីមេទ្រី និង/or ស៊ីមេទ្រីបង្វិល. បិទជិត គឺ ជា មាត្ររូប កញ្ចក់ ប្រសិន បើ ការ បង្វិល ភ្នែក មាន ឥទ្ធិពល ដូច គ្នា នឹង ការ បង្វែរ វា ជា ច្រើន ដង ។ ខ្វាក់ គឺ ជា ការ បង្វិល សមាមាត្រ ប្រសិន បើ ការ បង្វិល 90 ដឺក្រេ នីមួយ ៗ បន្សល់ ទុក នូវ ភាព ខ្វាក់ មិន ផ្លាស់ ប្តូរ ។
-
ខ្វាក់ បី នាក់ ក្នុង ល្បែង នេះ គឺ ជា ការ វាស់ ស្ទង់ កញ្ចក់ ។ ខ្វាក់ ពណ៌ ផ្កា ឈូក និង ពណ៌ ស្វាយ គឺ ជា យោគៈ តាម អង្កត់ផ្ចិត ហើយ ខ្វាក់ ពណ៌ ខៀវ គឺ ជា យោគៈ នៅ តាម ផ្តេក។ ខ្វាក់ ពណ៌ បៃតង មិន មែន ជា មាត្រិក កញ្ចក់ ទេ ។ សម្រាប់ ល្បែង នេះ វា មិន សំខាន់ ទេ ថា តើ អ័ក្ស ស៊ីស៊ី ដែល មាន ភាព ស្មើ គ្នា នៅ កន្លែង ណា ទេ ពីព្រោះ មួយ អាច បង្វិល ខ្វាក់ នីមួយៗ បាន ។



-
គ្មាន អ្នក ខ្វាក់ ណា ម្នាក់ នៅ ក្នុង ល្បែង នេះ គឺ ជា មាត្រមាត្រ បង្វិល ឡើយ ។ ខ្វាក់ ដែល មាន យោគ សិទ្ធ បែប នេះ (តែ មិន ត្រូវ បាន ប្រើ ក្នុង ល្បែង នេះ) រួម មាន បន្ទាត់ ត្រង់ ឬ រាង 'X' ។

-
ខ្វាក់ ភ្នែក ដោយ ឆ្លុះ ស្នែង មាន តែ រដ្ឋ ៤ ផ្សេង គ្នា ប៉ុណ្ណោះ ដែល ត្រូវ ពិនិត្យ មើល ដូច្នេះ រូបរាង ពណ៌ ផ្កា ឈូក ខៀវ និង ពណ៌ ស្វាយ នីមួយៗ មាន រដ្ឋ ចំនួន ៤។ ខ្វាក់ ភ្នែក ដែល មិន មាន ភាព ស្មើ គ្នា នៃ កញ្ចក់ មាន រដ្ឋ ប្រាំ បី ផ្សេង គ្នា ដើម្បី ពិនិត្យ មើល ។ ដោយសារ តែ ខ្វាក់ ពណ៌ បៃតង គឺ ជា មនុស្ស តែ ម្នាក់ គត់ ដែល មិន មែន ជា មាត្រិក វា គឺ ជា ការ ខ្វាក់ តែ មួយ គត់ ដែល មាន រដ្ឋ ប្រាំ បី ផ្សេង គ្នា ។ អ្នក អាច ពិនិត្យ មើល រឿង នេះ ដោយ សាកល្បង ការ បង្វិល នាឡិកា ទាំង អស់ របស់ មនុស្ស ខ្វាក់ ម្នាក់ ៗ ហើយ បន្ទាប់ មក បង្វិល វា ម្តង ទៀត ។
-
នៅ ពេល ដែល អ្នក ចាប់ ផ្តើម ដាក់ ខ្វាក់ នៅ លើ ក្ដារខៀន អ្នក មាន ចំណុច ៤ ផ្សេង គ្នា ដើម្បី ដាក់ កន្លែង ខ្វាក់ ដំបូង បន្ទាប់ មក ចំណុច ៣ ផ្សេង គ្នា សម្រាប់ ចំណុច ទី ពីរ ២ កន្លែង ផ្សេង គ្នា សម្រាប់ ចំណុច ទី បី និង ទី តាំង មួយ ដែល នៅ សល់ សម្រាប់ អ្នក ខ្វាក់ ចុង ក្រោយ ។ នេះ ទុក ឲ្យ យើង មាន 4 × 3 × 2 × 1 = 24 កន្លែង ដាក់ ។ ចំនួន នេះ ក៏ អាច ត្រូវ បាន គេ ហៅ ថា កត្តា ៤ ឬ ៤!.
ខ្វាក់ បំពង់ បី អាច ត្រូវ បាន បង្វិល បួន វិធី ផ្សេង គ្នា ដូច ដែល បាន បង្ហាញ ពី មុន ។ នេះផ្តល់ឱ្យយើងនូវចំនួនសរុប (4 × 4 × 4 ) × (4 × 3 × 2 × 1) = 1536 កន្លែងដាក់ផ្សេងៗ រហូតមកដល់ពេលនេះ។
ជាចុងក្រោយដោយសារតែខ្វាក់ពណ៌បៃតងអាចបង្វិលបានចំនួន ៨យ៉ាងខុសៗគ្នា យើងទទួលបានចំនួនសរុប (៨ × ៤ × ៤ × ៤) × (៤ × ៣ × ២ × ១) = ១២២៨៨ កន្លែងផ្សេងគ្នាសម្រាប់មនុស្សខ្វាក់។
-
បន្ទាប់ មក នឹង មាន ចំនួន សរុប (8 × 8 × 8 × 8 × 8 ) × (4 × 3 × 2 × 1) = 98304 កន្លែង ផ្សេង គ្នា សម្រាប់ អ្នក ខ្វាក់ ។
 សម្រាប់ 'n' ខ្វាក់ភ្នែកជាមួយ symmetry និង 'm' ខ្វាក់ភ្នែកដោយគ្មាន symmetry, ដើម្បីស្វែងរករូបមន្តដើម្បីគណនាចំនួននៃការដាក់ដែលអាចធ្វើទៅបាននៃមនុស្សខ្វាក់.
សម្រាប់ 'n' ខ្វាក់ភ្នែកជាមួយ symmetry និង 'm' ខ្វាក់ភ្នែកដោយគ្មាន symmetry, ដើម្បីស្វែងរករូបមន្តដើម្បីគណនាចំនួននៃការដាក់ដែលអាចធ្វើទៅបាននៃមនុស្សខ្វាក់.
-
សូមជម្រាបថា យើងចង់ស្វែងរកសរុបសម្រាប់ក្តារដែលមានភ្នែក ២០ មមឺត និងខ្វាក់ភ្នែក ៥ យ៉ាង។ ជំនួស ឲ្យ ការ សរសេរ ចេញ ពី 20 4 និង 5 8's ដូច ដែល យើង បាន ធ្វើ ពី មុន យើង អាច បង្កើត រូប មន្ត ដើម្បី ធ្វើ ឲ្យ ការ គណនា នេះ សាមញ្ញ ។
ពី ផ្នែក ខាង លើ យើង ដឹង ថា ចំនួន រដ្ឋ សម្រាប់ មនុស្ស ខ្វាក់ យោគ គឺ ៤. យើង ក៏ អាច មើល ឃើញ ថា សម្រាប់ មនុស្ស ខ្វាក់ ដែល មាន សាមគ្គី ភាព ចំនួន មួយ ចំនួន សរុប នៃ ការ ដាក់ គឺ 4n ដែល ' n ' គឺ ជា ចំនួន អ្នក ខ្វាក់ ដែល មិន សម រម្យ ។
ដូច គ្នា នេះ ដែរ យើង ដឹង ដែរ ថា ចំនួន រដ្ឋ សម្រាប់ ការ ខ្វាក់ ភ្នែក មិន សម រម្យ គឺ 8 ហើយ យើង ទទួល បាន ចំនួន សរុប នៃ ការ ដាក់ រហូត ដល់ ម៉ោង 8ព្រឹក ដែល ' m ' គឺ ជា ចំនួន អ្នក ខ្វាក់ ដែល មិន សម រម្យ ។
ដូចពីមុន ដើម្បីរកចំនួនសរុបនៃមធ្យោបាយដែលមនុស្សខ្វាក់អាចដាក់បាន (ដោយមិនរាប់បញ្ចូលការបង្វិល) ទៅលើក្តារនោះ យើងប្រើ s!, ជាមួយ 's' ជាចំនួនមនុស្សខ្វាក់។
ការ ពង្រីក ទាំង នេះ រួម គ្នា ផ្ដល់ ឲ្យ យើង 4n × 8m × s ! = t, where 't' ជាចំនួនសរុបនៃកន្លែងដាក់សម្រាប់មនុស្សខ្វាក់។
ចាប់ តាំង ពី2 2 = 4 និង 23 = 8 រូបមន្ត អាច ធ្វើ ឲ្យ សាមញ្ញ ដូច ខាង ក្រោម ៖
4n * 8m = (22)n * (23)m
= (22n) * (23m)
= 22n + 3m
នេះផ្តល់ឱ្យយើងនូវរូបមន្តចុងក្រោយ 22n + 3m × s! = t, where 'n' គឺជាចំនួននៃភាពខ្វាក់នៃ symmetrical' 'm' គឺជាចំនួននៃភាពខ្វាក់អាសមីត 's' គឺជាចំនួននៃចំនួននៃមនុស្សខ្វាក់ (ដែលអាចរកឃើញផងដែរជាមួយ n + m) ហើយ 't' គឺជាចំនួនសរុបនៃកន្លែងសម្រាប់ខ្វាក់ភ្នែក។ សូម សាកល្បង រូបមន្ត នេះ ដោយ ប្រើ លេខ សម្រាប់ ក្ដារខៀន នៅ លើ ទំព័រ បណ្ដាញ នេះ (មួយ ខ្វាក់ មាត្រមាត្រ និង ខ្វាក់ ៣) ។
ឥឡូវ នេះ ដែល យើង ដឹង ថា រូប មន្ត នេះ ត្រឹម ត្រូវ យើង អាច ស្វែង យល់ ពី ចំនួន កន្លែង ដាក់ សម្រាប់ ក្ដារ ដែល បាន រៀបរាប់ នៅ ដើម ផ្នែក នេះ ដោយ មាន មនុស្ស ខ្វាក់ 20 symmetrical និង 5 ។
22n + 3m * 25! = t
22(20) + 3(5) * 25! = t
240 + 15 * 25! = t
255 * 25! = t
5.59 x 1041 = t
(ចម្លើយពិតប្រាកដគឺ 558850238169687388730388679609024512000000 ឬ ៥រយ និង ៥រយ-៨ កោឌុល, ៨ រយ ហាសិប ហាសិប ១០រៀល ២រយ និង សាមសិបប្រាំបី ១រយ និង ៦០៩នាក់ ៦នាក់ និង ៨៨នាក់ ១០នាក់ ៣រយ-៨៨នាក់ ៧រយ និង ៨០នាក់ រួមភេទ ៣រយ-៨៨នាក់ ៦នាក់ និង ៧០៩នាក់ ៦នាក់ និង៩០០នាក់ ម្ភៃបួនពាន់លានប្រាំរយ ដប់ពីរលាន)
-
ខណៈ ពេល ដឹង ពី របៀប រក ចំនួន កន្លែង ដាក់ មិន ជួយ អ្នក ដោះស្រាយ ផ្គុំ រូប ក៏ នៅ មាន ប្រយោជន៍ នៅ ឡើយ។ ខណៈ ដែល យើង កំពុង អភិវឌ្ឍ ល្បែង នេះ យើង ចាំបាច់ ត្រូវ ប្រាកដ ថា សំណួរ នីមួយៗ មាន ដំណោះ ស្រាយ តែ មួយ ប៉ុណ្ណោះ ។ ដើម្បី ធ្វើ បែប នេះ ដំបូង យើង ត្រូវ តែ ស្វែង រក កន្លែង ដាក់ ដែល អាច ធ្វើ ទៅ បាន ទាំង អស់ សម្រាប់ ក្ដារខៀន ។ ដើម្បីទុកកន្លែងដាក់ទាំងនេះ យើងប្រើ array, ដែលមានទំហំថេរ។ យើង បាន ប្រើ រូបមន្ត ខាង លើ ដើម្បី កំណត់ ទំហំ អ្វី ដែល អារេ គួរ តែ មាន ។
-
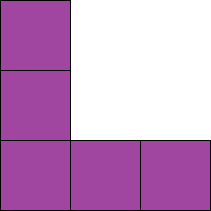
អ្នក ខ្វាក់ បួន នាក់ នៅ លើ ក្តារ នីមួយ ៗ មាន ការ៉េ តូច ៗ ។ ៣ ក្នុង ចំណោម នោះ ធ្វើ ពី ៦ ការ៉េ ហើយ មួយ ទៀត ធ្វើ ពី ៥។
រូបរាង ដែល បង្កើត ឡើង ដោយ ការ៉េ តូច ៗ មួយ ចំនួន ត្រូវ បាន គេ ហៅ ថា ប៉ូលីមីនូ ។ មាន លក្ខខណ្ឌ ជាក់លាក់ បន្ថែម ទៀត សម្រាប់ រូបរាង ដែល មាន ចំនួន ការ៉េ ជាក់លាក់ & # 160; ។ Hexominoes មាន ៦ ការ៉េ ហើយ ១២ មីណូ មាន ចំនួន ៥។
ហ្គេមល្បីៗជាច្រើនប្រើ ១២ មីណូ រួមមាន Tetris, Blokus, និង Dominoes។ ក៏ មាន កំណែ មួយ ចំនួន របស់ ស៊ូដូគូ ដែល ប្រើ ប៉ូលីមីនម៉ូស ជំនួស ឲ្យ ការ៉េ សម្រាប់ ក្រឡាចត្រង្គ ។
ព័ត៌មាន បន្ថែម អំពី polyminoes អាច រក បាន នៅ៖





Follow ឬ subscribe សម្រាប់ updates: