សុខ សោភា©
ចំនួនសរុបនៃការឈ្នះ៖: 166366
ការណែនាំអំពីរបៀបលេងល្បែង សូគូបាន
កំណត់ចំណាំ
លក្ខណ្ឌខាងក្រោមនឹងត្រូវបានប្រើក្នុងការណែនាំនេះ។
- ផ្លាស់ទីមួយជំហ៊ាននៃតួអង្គក្នុងល្បែងទោះបីជារុញឬទាញប្រអប់។
- គន្លង៖ ការផ្លាស់ប្ដូរជាបន្តបន្ទាប់
- ទីតាំង៖ បញ្ហាទាំងស្រុងជាមួយអ្នកលេងល្បែងនិង ប្រអប់ទាំងអស់ដែលស្ថិតនៅកន្លែងជាក់លាក់មួយ។
- ដំណោះស្រាយ៖ ទីតាំងដែលប្រអប់នីមួយៗស្ថិតនៅលើចំណុចមួយ។
- គន្លងដំណោះស្រាយ៖ លំដាប់នៃការផ្លាស់ប្តូរពីទីតាំងដើម ទៅកាន់ដំណោះស្រាយ។
- ទីតាំងស្លាប់៖ ជាទីតាំងដែលមិនអាចរកដំណោះស្រាយបាន។
យុទ្ធសាស្ត្រទូទៅ
ដំណោះស្រាយដ៏ខ្លីបំផុតអាចមាន ១០០, ៣០០ ឬសូម្បីតែផ្លាស់ទី១០០០ផ្លាស់ទី។(ល្បែងសាមញ្ញបំផុតទី១របស់យើងគឺត្រូវការផ្លាស់ទី៧៣ រួចហើយល្បែងទី៨ ត្រូវការផ្លាស់ទី១២៦)។ ប្រសិនបើមានតម្លៃមធ្យម នោះលទ្ធភាពមានពីរសម្រាប់ការផ្លាស់ទីនីមួយៗ ហើយដំណោះស្រាយត្រូវចំណាយពេល ១០០ផ្លាស់ទី បន្ទាប់មកស្វែងរកដំណោះស្រាយគន្លង ២^១០០ ដើម្បីរកដំណោះស្រាយ។ សូម្បីតែកុំព្យូទ័រក៏មិនអាចទៅរួចដែរ។ ដូច្នេះយើងចាំបាច់ត្រូវ៖
- ត្រូវដឹងជាមុន ប្រសិនបើទីតាំងស្លាប់
- បំបែកគោលដៅរួមទៅជាកិច្ចការរង។ ប្រសិនបើដំណោះស្រាយដោយផ្នែក ១០០ផ្លាស់ទី អាចត្រូវបានបំបែក ទៅជា១០ កិច្ចការរង នោះភាពស្មុគស្មាញនៃបញ្ហាត្រូវបានកាត់បន្ថយយ៉ាងខ្លាំង។ លើសពីនេះទៅទៀត វាអាចនឹងកាត់បន្ថយនូវលំដាប់ដែលកិច្ចការរងត្រូវបានបញ្ចប់ ហើយបន្ទាប់មកបញ្ហាទាំងមូល នឹងងាយស្រួលក្នុងការដោះស្រាយ។
- ស្វែងរកលក្ខខណ្ឌ ក្នុងគន្លងដោះស្រាយ
- ពិចារណាអំពីវិធីដោះស្រាយផ្សេងទៀត។
ករណីទី ១៖ ការទទួលស្គាល់ពីទីតាំងស្លាប់ជាមុន
១.១៖ ពេលខ្លះវាងាយស្រួលក្នុងការសម្រេចថាតើ ទីតាំងណាស្លាប់ឬអត់ មានតែសង្កេតមើលទៅលើអ្វីដែលនៅជុំវិញប្រអប់តែ១ប៉ុណ្ណោះ។ អ្វីទាំងអស់ដែលវាត្រូវការត្រួតពិនិត្យមើលគឺ “ទីតាំង”។ ប្រសិនបើប្រអប់មួយមិនស្ថិតលើចំណុចមួយ ហើយមិនអាចផ្លាស់ទីតាមជួរដេក និងមិនអាចផ្លាស់ទីតាមជួរឈរទេ នោះជាទីតាំងស្លាប់ហើយ។ ប្រអប់ត្រូវបានបិទដោយ ជញ្ជាំង ឬដោយប្រអប់ផ្សេងទៀតដែលមិនអាចផ្លាស់ទីបាន។
Examples:





១.២៖ វាពិបាកបន្តិចក្នុងការមើលថាទីតាំងមួយនិងស្លាប់ ប្រសិនបើប្រអប់នៅជាប់នឹងជញ្ជាំង ហើយវាអាចរុញបាន ប៉ុន្តែមានតែនៅតាមបណ្តោយជញ្ជាំងនោះតែប៉ុណ្ណោះ ហើយគ្មានកន្លែងណាដែលវាអាចទៅដល់ជាចំណុចនោះទេ។
Example:

ជាទូទៅប្រអប់នៅជាប់នឹងជញ្ជាំង ហើយអាចផ្លាស់ទីទៅកន្លែងដែល វាមិនមានជញ្ជាំងនៅចំហៀងបស់វា (កន្លែងAខាងក្រោម) ប៉ុន្តែកន្លែងជិតខាងAដែលទំនេរ មិនអាចផ្លាស់ទីដោយអ្នកលេងល្បេងរុញប្រអប់បន្ទាប់នៅជាប់ A។
Example:


ករណីទាំងបីនេះសម្រេចបាននៅមូលដ្ឋាន និងមិនចាំបាច់ផ្លាស់ទីអ្នកលេងល្បែង។ ដូច្នេះគេអាចពិនិត្យមើលទីតាំងដំបូង ហើយគេសម្គាល់កន្លែងដែលត្រូវបានហាមមិនឲ្យនិយាយជាមួយ ដូច្នេះប្រអប់មួយអាចនឹងមិនត្រូវបានរុញទៅកាន់កន្លែងបែបនេះឡើយ។
ជាទូទៅ កន្លែង A អាចទៅដល់ដោយអ្នកលេងល្បែង ប៉ុន្តែត្រឹមតែតម្លៃនៃការដាក់ប្រអប់មួយទៀត នៅកន្លែងហាមឃាត់។
Example:

ការពន្យល់នេះកើតឡើងដដែលៗ[1]វាមានលក្ខណៈជាទីតាំងស្លាប់ដោយប្រើពាក្យ ស្លាប់។ ទីតាំងស្លាប់បែបនេះគឺពិបាកក្នុងការទទួលស្គាល់ ព្រោះវាមិនអាចនឹងត្រូវបានរកឃើញ ដោយការត្រួតពិនិត្យទីតាំង ហើយប្រហែលជាត្រូវ ការការផ្លាស់ទីសាកល្បង។
ករណីទី ២ ៖ ការបង្កើតកិច្ចការរង
ឧទាហរណ៍កិច្ចការរងនោះគឺ
- ផ្លាស់ទីអ្នកលេងល្បែងពី A ទៅ B
- ផ្លាស់ទីប្រអប់ជាក់លាក់មួយពី A ទៅ B
កន្លែងដែលកិច្ចការនីមួយៗត្រូវបានសម្រេចដោយមិនបង្កើតទីតាំងស្លាប់។
ឧទាហរណ៍សម្រាប់ (a) ៖ តើអ្នកលេងល្បែងអាចហុចប្រអប់មួយយ៉ាងដូចម្តេច ដើម្បីទៅដល់ A ៖
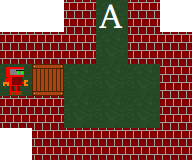 →
→
 →
→
 →
→
 →
→

លំហរទទេរទាំងអស់គឺ ត្រូវការជាចាំបាច់ព្រោះអ្នកលេងល្បែងត្រូវរុញជុំវិញប្រអប់។ ប្រសិនបើមានលំហទទេរតិចនោះអ្នកលេងល្បែងមិនអាចឆ្លងកាត់ប្រអប់ដោយមិនបង្កើតទីតាំងស្លាប់បានទេ។
ប្រសិនបើមានមនុស្សស្គាល់កិច្ចការរងបែបនេះជាមួយរូបរាងនៃច្រករហៀង ដោយរត់មាត់ នោះគេអាចសន្សំពេលវេលាបានច្រើន ដោយមិនចាំបាច់គិតពីវាទេ នេះជាគន្លងផ្លាស់ទី ទី៩ ។ សំខាន់ជាងនេះទៅទៀតគេមិនចុះចាញ់ទេ ព្រោះគេគិតថាកិច្ចការរងនេះគឺមិនអាចទៅរួច។
សំណួរទាក់ទងនឹងកិច្ចការរងគឺជាវិធីក្នុងការរកកិច្ចការរងទាំងនោះ។ ឧទាហរណ៍ កិច្ចការរងកើតឡើងនៅពេលដោះស្រាយបញ្ហាបញ្ច្រាស។ ឧបមាថាចំណុចជាក់លាក់មួយអាចទៅដល់បានតែម្ខាង ហើយបានតែប្រអប់មួយប៉ុណ្ណោះ។ ជាលទ្ធផលប្រអប់នេះត្រូវការរុញក្នុងទិសដៅជាក់លាក់មួយ។ ដើម្បីធ្វើដូច្នេះអ្នកលេងល្បែងត្រូវទៅម្ខាងទៀត។ កិច្ចការនោះអាចជាការនាំយកប្រអប់ និងអ្នកលេងល្បែងនៅក្នុងទីតាំងត្រឹមត្រូវ។
ឧទាហរណ៍ធម្មតាមួយទៀតនៃការបង្កើតកិច្ចការរងគឺដូចខាងក្រោម។ វាជារឿងធម្មតាក្នុងការសន្មត់ថាចន្លោះខាងក្នុងទាំងអស់នៅក្នុងទីតាំងមួយគឺត្រូវការនូវដំណោះស្រាយ។ នោះមានន័យថា ប្រសិនបើទីតាំងដើមមានចន្លោះខាងក្នុងធំ ដូចជាផ្ទៃទទេ 2 គុណ 3 ក្នុងឧទាហរណ៍ខាងលើ នោះគេអាចសួរថាតើគោលបំណងអ្វីសម្រាប់លំហនោះ។ អាចថា អ្នកលេងល្បែងត្រូវការវាដើម្បីហុចប្រអប់មួយ ឬវាត្រូវបានប្រើសម្រាប់រក្សាទុកប្រអប់បណ្ដោះអាសន្ន ដើម្បីទុកកន្លែងទំនេរនៅកន្លែងផ្សេងជាមធ្យម។ ដូច្នេះប្រសិនបើទំហំទំនេរធំនោះអាចរក្សាទុកប្រអប់មួយជាបណ្ដោះអាសន្ន តើប្រអប់នោះអាចជាប្រអប់មួយណា? តើគេអាចយកប្រអប់នេះទៅកន្លែងផ្ទុកកម្រិតមធ្យមដោយរបៀបណា?
អំពី 3: ការបង្កើតលក្ខខណ្ឌលើគន្លងវិធីដោះស្រាយ
មានលក្ខខណ្ឌជាច្រើននៅលើគន្លងវិធីដោះស្រាយដែលអាចធ្វើទៅបានដោយគ្រាន់តែមើលទីតាំងដោយមិនព្យាយាមផ្លាស់ទី។ ឧទាហរណ៍គឺ៖
3.1៖ មានច្រកតូចមួយដែលអាចចូលបានដោយប្រអប់ ប៉ុន្តែប្រអប់មិនអាចឆ្លងកាត់ច្រកនោះទាំងមូលបានទេ ដូច្នេះហើយចន្លោះនៅចុងបញ្ចប់នៃច្រកនោះមិនអាចទៅដល់ទីតាំងដែលច្រកមួយនោះបញ្ចប់ទេ។
ឧទាហរណ៍ ចំណុច A មិនអាចទៅដល់បានដោយប្រអប់ដែលកំណត់លើ B ហើយ B មិនអាចទៅដល់ដោយប្រអប់ដែលកំណត់លើ A ដោយឆ្លងកាត់ជ្រុង។
3.2៖ ចំណុចជាក់លាក់មួយអាចទៅដល់បានតែម្ខាងប៉ុណ្ណោះ ទោះបីជាមានលំហរទំនេរនៅសងខាងក៏ដោយ។
ឧទាហរណ៍ ចំណុចមិនអាចទៅដល់បានដោយប្រអប់ខាងក្រោម។
3.3៖ ប្រអប់ជាក់លាក់មួយមិនអាចផ្លាស់ទីក្នុងទិសដៅជាក់លាក់មួយបានទេ ដូច្នេះហើយអាចទៅដល់ចំណុចជាក់លាក់មួយប៉ុណ្ណោះ។
ឧទាហរណ៍ ប្រអប់អាចទៅដល់ចំណុចនៅលើផ្នែកខាងឆ្វេងរបស់វាប៉ុណ្ណោះ។
3.4៖ ដោយសារតែប្រអប់ អាចទៅដល់ចំណុចបានតែផ្នែកខ្លះប៉ុណ្ណោះ ដែលវាអាចកំណត់នូវលំដាប់ដែលចំណុចត្រូវស្ថិតនៅ។
ឧទាហរណ៍ នៅទីតាំងខាងក្រោម ចំណុចខាងឆ្វេងត្រូវតែស្ថិតនៅមុនចំណុចនៅខាងស្តាំរបស់វា។
3.5៖ វាអាចបញ្ជាក់ច្បាស់អំពីចំណុចណាដែលត្រូវស្ថិតនៅចុងក្រោយ ព្រោះអ្នកលេងល្បែងត្រូវការកន្លែងដើម្បីរុញប្រអប់ក្នុងទិសដៅជាក់លាក់មួយ។
ឧទាហរណ៍ ចន្លោះនៃចំណុចខាងស្តាំបំផុតគឺត្រូវការសម្រាប់អ្នកលេងល្បែងដើម្បីឈរ ហើយរុញប្រអប់មួយទៅខាងឆ្វេង ដូច្នេះចំណុចខាងស្តាំបំផុតគឺជាចំណុចចុងក្រោយដែលត្រូវស្ថិតនៅ (ក្នុងរូបភាពដូចខាងលើ)។អំពី 4៖ វិធីដោះស្រាយផ្សេងៗទៀត។
៤.១៖ រាល់ការរុញច្រានដែលអាចបញ្ច្រាស់បាន អាចនិងគួរត្រូវបានសាកល្បង ទោះបីជាវាមានន័យថា អ្នកលេងល្បែងត្រូវទៅផ្លូវឆ្ងាយ ដើម្បីរុញពីម្ខាងទៀតដើម្បីបញ្ច្រាសការរុញទាំងនេះ។ ទោះបីជាលំហាត់បែបនេះមើលទៅគ្មានន័យក៏ដោយ ក៏ទីតាំងថ្មីអាចបើកឱកាសឱ្យរកឃើញនូវលទ្ធភាពដោះស្រាយថ្មីៗក្នុងដំណើរការនេះ។
៤.២៖ ប្រសិនបើមានបន្ទាត់ត្រង់មួយដែលបែងចែកចំណុចទាំងអស់ចេញពីប្រអប់យ៉ាងតិចមួយ នោះប្រអប់នេះត្រូវតែឆ្លងកាត់បន្ទាត់នោះ។ បើមិនអាចធ្វើទៅបាន នឹងមិនមានទីតាំងណាកើតឡើងទេ។ ប្រសិនបើមានផ្លូវតែមួយសម្រាប់ប្រអប់ដើម្បីឆ្លងកាត់បន្ទាត់នោះ មានន័យថាគន្លងដំណោះស្រាយមានលក្ខខណ្ឌកំណត់តឹងរឹងមួយ។
ឧទាហរណ៍នៃដំណោះស្រាយពេញលេញ ល្បែងទី 8
 (1)
(1)
យើងណែនាំកូអរដោនេរដល់ចំណុចស្លាក។ ជាឧទាហរណ៍ អ្នកលេងល្បែងដំបូងស្ថិតនៅចំណុច G1។
ដំបូងឡើយ អ្នកលេងល្បែងមានជម្រើសតែ 2 ប៉ុណ្ណោះគឺ A ចូលតាមរន្ធ G3 ឬ B ដើម្បីចូលតាមរន្ធ E3។ ឆ្លងកាត់ G3 គ្រាន់តែអនុញ្ញាតឱ្យអ្នកលេងល្បែងរុញប្រអប់ B3 ទៅ B1 លទ្ធផលបណ្តាលឱ្យចាញ់។ ដូច្នេះលេងល្បែងឆ្លងកាត់រន្ធ E3 ទៅ B2:
 (2)
(2)
ការរុញតែមួយគត់ដែលយើងអាចធ្វើបានគឺ A, ប្រអប់ B3 រហូតដល់ B4 (មិនមែន B5 ដែលមានន័យថាចាញ់) ឬប្រអប់ C2 ទៅខាងស្តាំ។
យើងដឹងថាប្រអប់មិនអាចផ្លាស់ទីទៅចំណុចនៅលើផ្លូវឆ្លងកាត់ G3 បានទេព្រោះវាមិនអាចផ្លាស់ទីទៅខាងឆ្វេងនៅពេលក្រោយ ដូចដែលបានឃើញក្នុង 1.2 ។
ប៉ុន្តែដើម្បីផ្លាស់ទីពួកវាតាមរន្ធ B3, C3 យើងត្រូវការកន្លែងទំនេរនៅក្នុងតំបន់នេះ ដូច្នេះយើងត្រូវដាក់ប្រអប់មួយ ឬពីរនៅខាងស្តាំ ហើយត្រូវយកវាមកវិញនៅពេលក្រោយ។
យើងក៏ដឹងដែរថាប្រអប់ B3 អាចផ្លាស់ទីបានតែនៅលើបន្ទាត់ B ដូច្នេះទីបំផុតនឹងត្រូវបញ្ចប់នៅលើចំណុច B4 ។
ដើម្បីផ្លាស់ទីប្រអប់នៅពេលក្រោយនៅលើ C4 ហើយបន្ទាប់មករុញពួកវាទៅខាងស្តាំ អ្នកលេងល្បែងត្រូវតែអាចផ្លាស់ទីទៅ A4 ប៉ុន្តែដើម្បីទៅដល់ទីនោះពីខាងក្រោម ប្រអប់ B3 ត្រូវតែនៅ B2 ហើយចន្លោះ B3, C3, C2 ត្រូវតែទំនេរ ដូច្នេះពីរ ប្រអប់ត្រូវតែចេញពីផ្លូវ ហើយត្រូវចតនៅខាងស្តាំខាងក្រោម។
�
 (3)
(3)
ដោយរុញចុះក្រោម ប្រអប់A3 ឬB3ពុំមានការប្រែប្រួលទេ។ មានជម្រើសតែមួយគត់ដែលយើងនៅក្នុងទីតាំង2គឺរុញប្រអប់B3 ឡើងទៅដល់B4មុន ហើយបន្ទាប់មកប្តូរទៅទីតាំងទី3។ យើងបាន៖
 (4)
(4)
ឥឡូវនេះយើងអាចដំណើរការបានដោយរុញប្រអប់ C3 ចុះទៅ C2 ហើយផ្លាស់ទីជាមួយអ្នកលេងល្បែងជុំវិញដើម្បីរុញប្រអប់ F2 ទៅ G2 និង G3៖
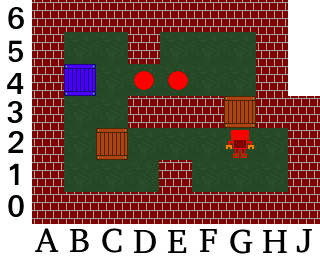 (5)
(5)
ដូចដែលបានពិភាក្សាខាងលើ យើងត្រូវការចន្លោះ B3, C3, C2 ឲ្យនៅទំនេរ ហើយយកប្រអប់ B4 ចុះទៅ B2 ដូច្នេះយើងត្រូវដាក់ប្រអប់ C2 ជាបណ្តោះអាសន្ននៅលើ G2សិន។ យើងបាន៖
 (6)
(6)
ឥឡូវយើងអាចធ្វើតាមផែនការដំបូងរបស់យើងហើយរុញប្រអប់ G2 ទៅកាន់ C4ដើម្បីរុញវាបន្ថែមទៀតឲ្យទៅខាងស្តាំ។
 (7)
(7)
សំណួរគឺថាតើយើងត្រូវរុញប្រអប់ C4 នោះដល់កម្រិតណា? ដោយសារតែយើងនៅតែត្រូវរុញប្រអប់ G3 ឆ្លងកាត់ផ្លូវដដែល យើងត្រូវយកអ្នកលេងល្បែងទៅ G4 ហើយដើម្បីធ្វើដូច្នេះយើងត្រូវរុញប្រអប់ C4 ដល់ F4 ហើយផ្លាស់ទីអ្នកលេងល្បែងទៅ G4 ដើម្បីរុញ G4 ទៅ G3។
 (8)
(8)
ដើម្បីផ្លាស់ទីប្រអប់ G2 ទៅខាងឆ្វេង អ្នកលេងល្បែងត្រូវដើរបញ្ច្រាសទ្រនិចនាឡិកាទៅ H2
 (9)
(9)
ក្រៅពីហ្នឹងគឺជារបៀបធម្មតា៖ រុញប្រអប់G2ចូលទៅ C2, C4, D4។
 (10)
(10)
បន្ទាប់មកប្រអប់ B2 ត្រូវបានរុញទៅ B4 ហើយបន្ទាប់មកទៀតអ្នកលេងល្បែងផ្លាស់ទីទៅ G4 ដើម្បីចុងក្រោយរុញប្រអប់ F4 នៅលើចំណុច E4 ។
បានធ្វើហើយ។
មានមនុស្សម្នាក់ត្រូវបានក្ស័យធន ប្រសិនបើបុគ្គលនោះជាម្ចាស់លុយនៃអ្នកផ្សេងទៀត ហើយអ្នកផ្សេងនោះមិនមានសាច់ប្រាក់ ហើយក៏មិនមានបង្កាន់ដៃសម្រាប់ការខ្ចីប្រាក់អ្នកដទៃ ឬក៏ពុំមានបង្កាន់ដៃសម្រាប់ការខ្ចីប្រាក់អ្នកផ្សេងដែរ ប៉ុន្តែបុគ្គលនោះបានក្ស័យធនហើយ។
ការពន្យល់នៃពាក្យក្ស័យធនដោយប្រើពាក្យក្ស័យធន ហើយនេះគេហៅវាថាប្រទាក់ក្រឡា។
ឧទាហរណ៍
បុគ្គល A,B,Cពុំមានប្រាក់ទេ ហើយពួកគេទាំងអស់ជំពាក់លុយបុគ្គល D
បុគ្គល Aមានបង្កាន់ដៃសម្រាប់ខ្ចីលុយពីបុគ្គល B
បុគ្គល Bមានបង្កាន់ដៃសម្រាប់ខ្ចីលុយពីបុគ្គល C
បុគ្គល Cមានបង្កាន់ដៃសម្រាប់ខ្ចីលុយពីបុគ្គល A
ប៉ុន្តែពួកគេគឺជាក្រុមដែលក្ស័យធនទាំងអស់។
ស្រដៀងគ្នាដែរតែខុសប្លែកត្រង់ស្ថានភាព៖
បុគ្គល A,B,Cពុំមានលុយនោះទេ ហើយពួកគេទាំងអស់ជំពាក់លុយបុគ្គល D
Aមានបង្កាន់ដៃសម្រាប់ខ្ចីលុយពីបុគ្គល B
Bមានបង្កាន់ដៃសម្រាប់ខ្ចីលុយពីបុគ្គល C
បុគ្គល Cមានបង្កាន់ដៃសម្រាប់ខ្ចីលុយពីបុគ្គល F
ដោយសារតែបុគ្គល Fប្រហែលនឹងមានលុយ ដូច្នេះវានឹងមិនមានបុគ្គលណាម្នាក់នៃ A,B,Cក្ស័យធនឡើយ។
ដើម្បីញែករវាងករណីពីរ។ ករណីមួយត្រូវការមើលរាល់ទំនាក់ទំនងទាំងអស់ហើយមិនត្រឹមតែបុគ្គលម្នាក់នោះទេ តែវាអាស្រ័យលើនិយមន័យនៃពាក្សក្ស័យធនខាងលើដែលវាប្រទាក់ក្រឡាគ្នា។





Follow ឬ subscribe សម្រាប់ updates: