Chomp ©

300000

Chomp

Pyeslərin ümumi sayı: 1644375
Qaliblərin ümumi sayı: 142050

Necə oynamaq lazımdır:

Oyun iki oyunçu ilə oynanılır, ya siz və bir dostunuz, ya da siz kompüterə qarşı.
Hər bir oyunçu növbə ilə aşağıdakı şəbəkədən konfet götürəcək.
Bir konfet seçildikdə, həmin konfetin aşağıda və sağ tərəfindəki bütün konfetlər də da çıxarılır.

Necə qazanmaq lazımdır:

Yuxarıdan ən soldakı konfeti götürən oyuçu oyunu uduzur.

1-ci oyunçunun növbəsi

iChomp oyunu üçün 'Bəzi yeməklər düşüncə üçün' (SFFT) giriş online shop satın alına bilər

Əgər siz sadəcə oyunda mümkün qədər sürətli olmaq istəyirsinizsə, onda 'Necə oynamaq haqqında daha çox' >> 'Kompüter ilə mövqeləri itirməyi necə öyrənmək ? ' ilə irəli gedin.

Bəzi düşündürücü məaqamlar çətinliyinə görə fərqlənir. Onlardan bəziləri ibtidai sinif şagirdləri üçün münasibdir, məsələn, "Bir şeyi sınayaq". Digər maddələr riyazi isbatları və onlardan əldə edilən faydanı nümayiş etdirir. Bu, orta məktəb materialıdır. Zəhmət olmasa, özünüz, yaxud Caribou Məktəb Riyaziyyat Clubunuz üçün nəyin uyğun olduğuna baxın.

Sualların cavablarını genişləndirməzdən əvvəl bir müddət düşünərək fəaliyyətlərdən maksimum fayda əldə edirsiniz.

Xoş əyləncələr.

Başlamaq üçün Bəzi Təriflər

Gəlin bir şeyi sınayaq

Gəlin, asan problemlərdən başlayaq, yəni kiçik mövqelər. Onları yaratmaq üçün 'Kompüter: Söndürülmüş' düyməsinə basırıq. Əgər (2,1) üzərinə klikləsək, yalnız xanaların bir sətri qalır.

Növbəti oyunçu, yəni rəqibiniz nə edə bilər?
- (1,2) üzərinə kliklədikdə, yalnız (1,1) xanası qalır və siz uduzursunuz.

Gəlin, 2-ci sətirdə bir xanaya və 1-ci sətrin hamısına sahib olmaq üçün "Yeni Oyun" və (3,1) və (2,2) üzərinə klikləyək.

Növbəti oyunçu nə edə bilər?
- (1,3) basmaqla cəmi üç xana qalır. Heç bir şansınız olmadığını görə bilirsiniz?

'Yeni oyun' və (3,1) və (2,3)-ə klikləyin.

Növbəti oyunçu nə edə bilər?
- Rəqibiniz (1,4)-ə klik edə bilər. Heç bir şansınız olmadığını görə bilirsiniz?

Cəmi 2 sətirdə xanalar olan hansı mövqelərdə oyunu qazanmaq şansınızın olmadığını ümumiləşdirə bilərsiniz?
- Əgər üst sətirdə 2-ci sətirdəkindən bir dənə çox xana varsa, o zaman nə etsəniz də, rəqibiniz hər zaman bir hərəkət edə bilər ki, üst sətirdə 2-ci sətirdəkindən 1 dənə çox xana olsun. Sonra nə etsəniz də, sonda (1,1) xanasını seçməli və oyunu uduzmalısınız.

Əgər bir xanaya klikləsəz, aşağıda və sağ tərəfdəki bütün xanalar da gedəcək. Bu qayda simmetriyaya malikdir; i.e. bütün oyunun aşağıdakı simmetriyası var: Əgər sətir və sütunları dəyişsək, qayda yenə də eynisini deyəcək: sağdakı bütün xanalar aşağıdakı xanalara çevrilir və aşağıda olan bütün xanalar çıxarılan xananın sağındakı xanalara çevrilir. Başqa sözlə, əgər biz (1,1) və (2,2) xətti boyunca hansısa mövqeyi güzgüyə əks etdirsək, onda yeni mövqe fərqli görünə bilər, amma eyni statusa malikdir. Qazanan hərəkət də eyni hərəkət olacaq, güzgü əksi kimi.

Birinci sırada 3 xana, ikinci sırada isə 2 xana olan mövqe, bildiyimiz kimi ümidsizdir. Güzgüdəki mövqelər hansı xanalara malikdirlər?
- 2-ci sütunda 3, 2-ci sütunda isə 2 xana olur.

Biz yalnız ilk iki cərgədə xanalar olan bütün ümidsiz mövqeləri bilirik. Simmetriya bizə yalnız ilk iki sütunda xanalar olan bütün ümidsiz mövqelər haqqında nə deyir?
- İlk iki sütunda xana olan ümidsiz mövqelər birinci sütunun ikinci sütundan bir qat daha çox olduğu yerlərdir.

Burada ümidsiz başqa bir mövqe də var: 'Yeni oyun' və (4,1), (2,2) və (1,4) klikləyin.

Əgər rəqib bu mövqedə addım atarsa, sizin cavabınız nədir?
- Hərəkət etdikdən sonra üst sətrin və birinci sütunun yenidən eyni uzunluqda olmasına diqqət etmək lazımdır. Bu nümunəni təkrar etməklə rəqib sonda (1,1) xanasını götürüb uduzacaq.

Beləliklə, əgər birinci sətir və birinci sütun eyni sayda xanalara malik olarsa və başqa xanalar yoxdursa, onda mövqe yararsızdır. Hansı mövqeləri belə bir mövqe ilə dəyişmək olar?
- Əgər bir mövqe eyni sayda sətir və sütuna malikdirsə, başqa yerdə nə qədər xana olursa olsun: bir hərəkət (2,2) sadəcə birinci sətri və bərabər uzunluqda birinci sütunu tərk edir, rəqibə heç bir şans qalmır. Beləliklə, əgər bir mövqedə sol sütunda olduğu kimi yuxarı sətirdə eyni sayda xana varsa, onda (2,2)-də oynayırsınız və oyunda qalib çıxırsınız.

Bəzi teoremlər və isbatlar

Chomp'u yaxşı oynamaq üçün qalib gəlmək və mövqeləri itirmək haqqında bilməlisiniz. Qalib mövqe odur ki, əgər biri digər tərəf nə etsə də, optimal oynayırsa, qələbəni həyata keçirə bilər. İtirən mövqe, əgər o biri tərəf optimal oynayırsa, birinin şansı olmayan mövqedir. Aşağıdakı nöqtələr riyaziyyatda bir tərif adlandırdıqları nöqtələrdir. Çompda uduzma və qalib mövqelər bu 3 pillə vasitəsilə müəyyən edilir:
1. Əgər yalnız bir xana qalırsa (yuxarı sol küncdə), onda bu, itirilə bilən mövqedir.
2. Əgər rəqib üçün uduzan mövqe ilə nəticələnən bir hərəkət varsa, mövqe qalib mövqedir.
3. Hər bir hərəkət rəqib üçün qələbə mövqeyi ilə nəticələnsə, mövqe uduzma mövqeyidir.
İlk baxışdan yuxarıdakı məqamlar faydasız görünə bilər, çünki qalib gələn mövqelər mövqeləri itirməklə izah olunur. Mövqeləri itirmək isə mövqelərin qalib gəlməsi ilə izah olunur. Buna baxmayaraq, təsnifat hərəkətlərin yerinə yetirilməsinə əsaslanır və hər bir hərəkət ardıcıllığı sonda tək bir xana mövqeyinə gətirib çıxarır ki, bu da 1-ci nöqtəyə görə, uduzulan mövqedir.

Heç bir tərəfin qalib ola bilməyəcəyi mövqelərin olması mümkündürmü? (çətin)
- Kiçik bir teorem tərtib edib onu sübut edəcəyik. Bu isbat bizə mükəmməl oyun gücünə çatmağın yolunu göstərəcək. İsbat induksiya yolu ilə isbat edilir, burada göstərmək istəyirik ki, əgər isbat etmək istədiyimiz ifadə N sayda xana üçün doğrudursa, birdən çox xana üçün də doğru olmalıdır, N+1 xana. N=1 xanaolduğu halda bu, N+1=1+1=2 üçün də doğru olmalıdır. N=2-nin doğru olması üçün N+1=2+1=3 xananın olması da həmçinin doğru olmalıdır; istənilən sayda xana üçün.
- Lemma (kiçik teorem): Hər bir mövqe ya qalib, ya da uduzan mövqedir.
- İnduksiya ilə isbat:
- İnduksiya Bazası: Mövqeydə yalnız bir xana varsa, bu xana yuxarı sol küncdədir və Chomp qaydasına uyğun olaraq mövqe itirilən mövqedir (yalnız N=1 xana olduqda lemmanın doğru olduğunu göstərir).
- İnduksiya hipotezi: Biz hesab edirik ki, lemma N xanasına qədər olan bütün mövqelər üçün doğrudur, yəni 1,2,..., N xana olan mövqelər ya qalib olur, ya da uduzur.
- İnduksiya addımı: İndi göstərmək istəyirik ki, bundan sonra N+1 xanaları ilə də bütün mövqelər ya uduzmalıdır, ya da qazanmalıdır.
- Aşağıda P N+1 sayda xana ilə ixtiyari bir mövqedir. Əgər P bir hərəkətlə azaldılırsa, onda yeni mövqe ≤N xanaları olmalıdır, buna görə də induksiya hipotezinə, əsasən, uduzma və ya qalib mövqedir. Əgər P bir hərəkətdə uduzan mövqeyə qədər azaldıla bilərsə, onda P qalib mövqedir. Əgər belə deyilsə, onda P bir hərəkətdə yalnız qalib mövqeyə endirə bilər. Amma əgər yalnız qalib mövqeyə keçməkdə mövqeyi azaltmaq mümkündürsə, onda P uduzduğu mövqe olmalıdır. Bu da sübut edir ki, P (N+1 sayda xanaların olması) ya qalib, ya da uduzan mövqedir. Bu,onu göstərir ki, bütün mövqelər (N+2,N+3 ilə,... xanalar) ya qalib gəlmək, ya da uduzmaqdır.
  
  İsbatların sonu ∎
- Əlavə Şərh: İnduksiya addımı bütün mövqelərə (müəyyən ölçülərə qədər) qalib gəlib-gəlməmələrinə və ya mövqelərini itirmələrinə qərar vermək üçün bir metod təqdim edir. Aşağıdakılar ilə müəyyən edilir:
  
  Biri N=1 ilə başlayır və bu mövqeyi uduzan mövqe kimi işarə edirlər. Sonra biri 2 xana ilə, sonra 3 xana və s. ilə bütün mövqelərin statusunu müəyyən edir, hər dəfə kiçik çmövqelərin statusunun bilgilərindən istifadə edir və yeni tapılmış uduzan mövqeni məlum olan mövqelərin siyahısına əlavə edir.
- Bu, müəyyən ölçüyə qədər bütün qalib və uduzan mövqeləri tapmaq üçün çox effektiv bir yoldur. Rəqəmlərin ölçüsü böyüdükcə, kompüter proqramı bizə kömək ola biləe. Zəruri izahlar aşağıdakılardır:
  - Prosedur N xanalardan az olan bütün mövqeləri bilməklə N xanalarının bütün mövqelərini səmərəli şəkildə yarada bilər.
  - Prosedur bir mövqenin başqa bir mövqeyə endirilə biləcəyini effektiv şəkildə yoxlaya bilir.
  Bu barədə daha çox düşünmək və bəlkə də belə bir kompüter proqramı yazmaq üçün onu sizə buraxacağıq.

Neçə məğlub və qazanan mövqedə tam olaraq 2 xana var?
- Cəmi iki mümkün mövqe var ki, onların da tam 2 xana, üst sətirdə 2 xana və ya sol sütun boyunca iki xana var. Bu mövqelərin hər ikisi qalib mövqelərdir.

Neçə uduzan və qalib gələn mövqedə tam olaraq 3 xana var?
- Tam 3 xana olan 3 ümumi mümkün mövqe var. Onlar 2 qalib mövqedən və 1 uduzan mövqedən ibarətdir. Onların hansı mövqe tutduqlarını müəyyən edə bilərsinizmi?

Neçə uduzan və qalib gələn mövqelərin dəqiq 4 xanası var?
- Burada 4 xana olan 5 mümkün mövqe var. Bu mövqelərin hamısı qalib mövqelərdir.

Neçə uduzma və qalib mövqelərdə dəqiq 5 xana var?
- Burada 5 xanası olan mümkün 7 mövqe var. Bu mövqelərdən 3-ü uduz, 4-ü isə qazanır. Onların hansı olduqlarını müəyyən edə bilərsinizmi?

Düzbucaqlı mövqelər qalibdir, yoxsa uduzan?
- Bu suala aşağıdakı lemma cavab verir. İsbat mövcudluğun isbatıdır . Bu hərəkətin nə olduğunu göstərmədən yalnız qələbə addımının mövcudluğunu isbatedəcək. Bununla belə, aşağıda izah edildiyi kimi, lemmanı bilmək oyununuz üçün faydalıdır.
- Lemma: 1-xana mövqeyi istisna olmaqla bütün dördbucaqlı mövqelər qalib mövqelərdir.
- İsbat: Bunun doğru olduğunu göstərmək üçün iki mümkün halı nəzərdən keçirmək lazımdır:
  1. Lövhənin aşağı sağ küncündəki xananı çıxarmaq qalib addımdır.
  2. Sağ aşağı küncdə olan xananı aradan qaldırmaq qalib bir hərəkət deyil.
- Əgər 1-ci hal doğrudursa, onda bu, o deməkdir ki, dördbucaqlı qalib mövqedir və bu lemmanı dəstəkləyir.
- Əgər 1-ci hal doğru deyilsə, onda 2-ci halı nəzərdən keçirmək lazımdır. Daha əvvəl etdiyimiz isbata görə, aşağı sağ küncdəki xananın çıxarılması nəticəsində yaranan mövqe qalib mövqe olmalıdır, yəni, onun mövcud qazanılmış addımı olmalıdır. Lakin, düzbucaqlıdakı hər bir hərəkət aşağı sağ küncdəki xananı çıxardığı üçün, o, 2-ci gediş (qalib hərəkət) nəticəsində yaranan mövqeyini itirir, istər künc hərəkətindən sonra, istərsə də künc hərəkəti əvəzinə qazanan hərəkət eynidir.
- İsbatların Sonu ∎
- Əlavə Şərhlər: Lemma bizə qələbə addımının nə olduğunu deməsə də, artıq dördbucaqlı mövqelərin qalib mövqelər olduğunu bilmək faydalıdır. Buna görə də, 1x1 mövqeyi istisna olmaqla, düzbucaqlı mövqe yaradan hərəkət etmək olmaz.

Qələbə addımının nə olduğunu hər hansı bir kvadrat lövhə üçün müəyyən edə bilərsinizmi?
- >1 böyüklüyündə olan bütün kvadratlar üçün yeganə qalib hərəkət (2,2)-dir.

Kvadrata bənzər hansı mövqelər üçün eyni addım qələbə addımıdır?
- Bu hərəkət (2,2) həmçinin 1-ci sətir və 1-ci sütunun eyni uzunluqda olduğu hər hansı bir mövqe üçün qazanılan addımdır.

Bir mövqedə birdən çox qələbə addımı ola bilərmi?
- Bəli, bir mövqe daha birdən çox qələbə addımı ola bilər. Gəlin növbəti mövqeyə nəzər salaq:
  
  ###
  ##
  #
  
  Bu lövhə mövqeyində edilə bilən 3 müxtəlif qalibiyyət hərəkəti var. Onların nə olduğunu müəyyən edə bilərsinizmi?

Oyunu Necə Oynamaq Haqqında Daha Ətraflı

Chomp'da qalib gəlmək üçün ümumi strategiya rəqibiniz üçün uduzan mövqelər yaratmaqdır ki, onların heç bir şansı olmasın. Biz həmçinin rəqibin bizim üçün uduzduğu mövqelərə dönə biləcəyi qalib mövqelər yaratmamaq istəyirik.

Qazanmağın açarı mümkün qədər çox itirən mövqeləri bilmək və rəqibinizdən əvvəl bir mövqe yaratmağın yolunu tapmaqdır. Məlum bir uduzma mövqeyi olan aşağıdakı lövhəni nəzərdən keçirək:

#######
###
###
#
#
Şəkil 1
Bir gedişlə bu itirilən mövqeyə çevrilə biləcək bütün mövqelər hansılardır?
- Yuxarıdakı itirmə mövqeyi aşağıda + işarəsi ilə işarələnmiş hər hansı bir hərəkət nəticəsində yarana bilər:
  
  #######+
  ###
  ###
  #
  # #######
  ###+
  ###
  #
  # #######
  ###
  ###
  #+
  # #######
  ###
  ###
  #
  #
  +
  
  Şəkil 2
  
  Bütün bu hərəkətlər kəsilmiş künclərdə yerləşir. Hər hansı bir belə + hərəkət aşağıdakı şəkillərdə görünə biləcək xanaları da ?: ilə kəsəcək:
- #######+?
  ###
  ###
  #
  # #######
  ###+???
  ###????
  #
  # #######
  ###
  ###
  #+?
  #?? #######
  ###
  ###
  #
  #
  +
  ?
  
  Şəkil 3
- + xanaları mütləqdir, ? xanaları isə seçimə bağlıdır. Sol qalib mövqedə, üst sətri daha çox '?' ilə elə belə sağa uzatmaq olar. Sağ qalib mövqedə isə birinci sütunu daha çox '?' ilə aşağıya uzatmaq olar. Bunların hamısı qalib mövqelərdir. Əgər belə bir mövqedə hərəkət etmək istəyiriksə , bir + xanası alacağıq və buna görə də bütün ? bağlı xanalar da götürüləcək, nəticədə başladığımız mövqe itiriləcək.

Daha çox qalib və ya daha çox uduzan mövqelər varmı?
- Hər itirilən mövqe üçün bir hərəkətlə bu itirilən mövqeyə çevrilə bilən sonsuz sayda mövqelər var. Bu sonsuz sayda mövqelərin hamısı buna görə də qazanan mövqelərdir.
- Buna görə də, mövqeləri itirməkdən daha çox qazanan mövqelər var. Buna görə də, mümkün qədər çox itirilən mövqeləri xatırlamaq ən təsirli olur, bütün digər mövqelər qazanan mövqelərdir.

Bildiyiniz uduzmuş mövqelərin siyahısını tərtib edin və hər bir mövqe üçün bütün müvafiq qalib mövqeləri və onların necə aşkar ediləcəyini yazın.
- Aşağıdakı nümunə nəyi nəzərdə tutduğumuzu göstərir:
- Daha əvvəl göstərildiyi kimi, mövqeyin cəmi 2 sətri olduqda və üst sətir ikinci sətirdən bir xana artıq olduqda bu, aşağıda göstərildiyi kimi itirilmə mövqeyi olur:
- #####
  ####
- Məlum olan bu uduzma mövqeyini götürərək, müvafiq qalib mövqelərin aşağıdakılar olduğunu müəyyən edə bilərik:
- #####+?
  #### #####
  ####+ #####
  ####
  +???
  ????
- Sol mövqedə hər hansı bir ədəd ola bilər ? yuxarı sətrin sağ tərəfində, düzgün mövqedə isə hər hansı bir sətir ola bilər ? Biz bu qalib mövqeləri necə aşkar etmək üçün söz ilə qısa məlumat verə bilərsiniz (hansı ki, sizin oyun üçün yadda saxlamalısınız):
- - Mövqe azalan qalib mövqedir
    #####
    ####
  - - Əgər mövqedə yalnız iki sətir var və birinci sətir tam bir xana çox deyil, sonra ikinci sətir, və ya
  - - Əgər mövqedə yalnız iki sətir varsa və birinci sətir tam olaraq bir xanadan çox deyilsə, ikinci ətirs, və ya
- Amma düşünmək üçün daha çox şey var. Biz bu cür qalib mövqelərdə düzgün oynamaqla bərabər, belə qalib mövqelər yaradan bir addım atmamaq istəyirik. Bu o deməkdir ki, biz cəmi iki sətir qaldığı yerdə və ya ikinci sətrin tam bir xana az olan,sonra birinci sətrə malik olduğu yerdə hərəkət etməməliyik.
- Qısaca ifadə etmək üçün, biz uduzan mövqelər yaratmaq istəyirik, eyni zamanda, uduzan mövqedən bir addım uzaq olan mövqelər yaratmamaq istəyirik.
- Başqa bir şeyi də qeyd etmək lazımdır: yuxarıda qeyd olunan güzgü simmetriyasına görə yuxarıda qeyd olunan bütün şərhləri sadəcə "sətir" sözünü "sütun" sözü ilə əvəz etməklə təkrar etmək olar.
- Daha çox uduzan mövqeləri və onların bir addım uzaqlaşan müvafiq qalib mövqelərini toplamaq sizə qalır.

Bəs əgər uduzduğun mövqedə oynamaq lazımdırsa, onda necə?
- Əgər siz başa düşürsünüzsə ki, uduzan mövqedə hərəkət etməlisiniz, onda nəzəriyyəyə görə sizin heç bir şansınız yoxdur. Yalnız ümid edə bilərsiniz ki, rəqibiniz növbəti addımınızla yarada biləcəyiniz mövqelər üçün bütün uduşlu hərəkətləri bilmir. Nə edə bilərsiniz yalnız bir kisəni bir küncdən çıxarın. Bu, rəqibinizə maksimal ölçüdə nəticə verən mövqe verir və rəqibinizin müvafiq qələbə addımını bilməsini daha da çətinləşdirir.

Mövqeləri təkbaşına itirməyi necə öyrənmək lazımdır?
- Tam ağac axtarışı kimi tanınan işləri yerinə yetirmək lazımdır. Birinci oyunçu bir hərəkəti təxmin etməklə başlayır, sonra ikinci oyunçu bir hərəkət təxmin edir və s. Bir oyunçu, oyunçu A, qalib gələnə qədər. Sonra oyunçu B onların etdikləri son addımı dəyişdirməyə icazə verilir və növbəti oyunçu A-nın növbəsidir. Əgər bir mövqedə növbəti oynayan oyunçu, B deyin, bütün hərəkət bir itkiyə gətirib çıxarır üçün hərəkətləri qurtarır, o zaman bu itkin mövqeyi. Oyunçu B bu itkin mövqeyi çatmamış edilən son hərəkət dəyişə bilər.
- Bu 'ağac axtarışı' başlanğıc mövqeyinin uduzduğu mövqe və ya 1-ci oyunçunun hansı hərəkəti onu itirmə mövqeyinə çevirəcəyi aydın olana qədər davam edir.
- Əgər kimsə bunu bir çox xana ilə ilkin lövhədə etməyə çalışırsa, bu çox uzun bir proses ola bilər. Lakin nə qədər çox itirdiyimiz mövqelər belə bir mövqeyə çatmamış hərəkətlərin ardıcıllığı bir o qədər qısadır və beləliklə, bütün axtarışlar daha sürətlidir. Əgər hər şeyin uduzduğu mövqelərin olduğunu bilsəydik, onda ya başlanğıc mövqeyi itirmə mövqeyi kimi qəbul edilərdi, ya da onu itirən mövqeyə endirmək üçün yalnız bir addım lazım olardı.

Kompüterlə mövqeləri itirməyi necə öyrənmək lazımdır?
- Çətinlik səviyyəsində 'Çox Çətin' və 8 x 15-dən böyük olmayan mövqelərdə kompüter mükəmməl oynayır. Belə ki, kompüterin hərəkətindən nəticə əldə edən hər bir mövqe məğlub mövqedir! Biri çox kiçik lövhələrdən başlamalı və kompüterə qarşı 'Çox Sərt' səviyyədə oynamalı və kompüterin meydana gətirdiyi bütün mövqeləri öyrənməlidir. Hər bir belə mövqe üçün düşünün ki, hər bir hərəkətinizə kompüter yenidən daha kiçik itki mövqeyinə çevirərək necə cavab verəcək. Hər bir itən mövqe üçün də əksi olan mövqe (sətir <--> sütunlar) məğlub mövqedir.
- Optimal ilk hərəkət nədir?
  - Müsabiqədə başlanğıc mövqe konfetlərin refraktoru olacaq. Daha əvvəl də sübut edildiyi kimi, reqütbu qələbəlik mövqedir. Bəs onu rəqib üçün uduzan mövqeyə dəyişən ilk addım nədir? Bir qədər əvvəl öyrəndik ki, kvadrat üçün optimal hərəkət (2,2) xanasıdır. Bəs əgər düzbucaqlı deyilsə, onda necə?
  - Sadəcə olaraq 'çox sərt' çətinlik səviyyəsinə dəyişin və kompüterin ilk addımı atmasına icazə verin. Nə qədər ki, dördbucaq 8x15-dən böyük deyil, kompüter optimal oynayır və mükəmməl birinci hərəkəti göstərəcək. Müxtəlif dördbucaqlı ölçüləri cəhd edin və optimal ilk hərəkəti yadda saxlayın, çünki kompüter :) müsabiqə günlərində mövcud olmayacaq.
- Tezliklə asan və orta çətinlik səviyyəsində məğlubedilməz olacaqsınız.

Mövqelərini itirən sonsuz ailələr varmı?
- Biz artıq bu iki ailə ilə tanış olduq. N hər hansı müsbət tam ədəddir.
- Daha ətraflı:

Kompüter oyunçusu necə işləyir?

Chomp Ətrafında Daha Çox Riyaziyyat (Orta Məktəb Səviyyəsi)

Aşağıdakı şərhlər Chomp'da güclənməyinizə kömək etməyəcək, lakin onlar bəzi maraqlı faktlar təqdim edəcək və induksiya ilə sübutları praktikada tətbiq etmək üçün bizə daha bir imkan yaradacaq.

Boş lövhə də daxil olmaqla, neçə fərqli mövqe P sətir və Q sütunları ilə bir düzbucaqlıya sığışır?
- Əgər boş refraktoru daxil etsək, aşağıdakı düsturdan istifadə etməklə mümkün olan mövqelərin ümumi sayını hesablaya bilərik: \[\frac{(P+Q)!}{P!Q!}\]Bu ədədi kiçik P və Q üçün hesablamaq və onun düzgünlüyünü yoxlamaq olarmı?
- Rekursiv Düsturun İlk Törəməsi
  - Qoy f(P,Q) ölçüsü PxQ olan düzbucaqlıdakı mövqelərin sayı olsun. Vacib müşahidə ondan ibarətdir ki, bütün mövqelər pilləkən formasına malikdir. Burada hər bir cərgədə ən çox yuxarıdakı cərgə qədər xana olur, amma daha çox deyil.
  - Əvvəlcə bütün bu pillələri təmsil edə biləcəyimiz bir yolla başlayaq. Asanlıqla pilləkən yaratmağın yollarından biri lövhənin sol alt küncündən başlamaq və ya sağa və ya yuxarı hərəkət etməkdir. Bu düz və yuxarı hərəkətləri lövhənin yuxarı sağ küncünə çatana qədər davam etdirmək olar. Biz bunu (P,0) -dan (0,Q) əldə etmək üçün keçdiyimiz yol kimi adlandıracağıq.
  - Mövqelərin sayı (P,0) -dan (0,Q)-yə qədər olan yolların sayı ilə eynidir, nə qədər ki, bir nəfərin yalnız yuxarı və ya sağa doğru hərəkət etməsinə icazə verilir. (P,0)-dan (0,Q+1) əldə etmək üçün yolların sayı f(P,Q+1), f(P,0) -dan (P,0) əldə etmək üçün yolların sayı f(P,Q),( 0,Q), sonra isə (0,Q+1) + f(P-1,Q) sıralarına qədər (P,0) -dan (P,0) (P,0) -a (1,Q), sonra isə (1,Q) və sonra (1, Q+1) və (0,Q+1) və s. Müvafiq formul aşağıdakı kimidir:\[f(P,Q+1) = f(P,Q) + f(P-1,Q) + f(P-2,Q) + \ldots + f(1,Q) + f(0,Q)\]
  - İndi bu düsturu götürüb P-i P + 1 ilə əvəz edəcəyik. P + 1-i P əvəzinə düsturda yerinə qoysaq, aşağıdakıları əldə edirik: \[f(P+1,Q+1) = f(P+1,Q) + f(P,Q) + f(P-1,Q) + \ldots + f(0,Q)\] \[f(P+1,Q+1) = f(P+1,Q) + f(P,Q+1)\]Bu yeni törəmədən düsturu təyin edə bilərik \(f(P,Q) = f(P,Q-1) + f(P-1,Q)\) harada \(f(P,0) = 1\) və \(f(0,Q) = 1\).
- Rekursiv Düsturun Alternativ Törəməsi
  - Çox vaxt kombinəatorial problemlərdə saymağın bir neçə üsulu olur. Aşağıdakı törəmə düsturunu əldə etmək üçün fərqli və daha zərif bir yol təqdim ediləcək.
  - Əvvəllər istifadə etdiyimiz eyni təsvirdən istifadə edəcəyik. Burada bizi (P,0) -dan (0,Q)-yə aparan halların ümumi sayını tapmaq istəyirik. Bunları iki qrupa bölə bilərik.
  - İlk gedişlə başlayan hal (P,0) -dan (P,1)-ə sağa doğru gedir. Biz bilirik ki, bu qrupda ümumi f(P,Q-1) qədər halımız (P,1) –dən (0,Q)-yə qədər olacaq. Biz bunu ona görə bilirik ki, birini sağa doğru hərəkət etdirdikdən sonra qalan düzbucaqlı P x ölçüsündədir (Q-1).
  - Digər qrup isə birinci hərəkətlə başlayır. Bu halda bir hərəkətdən (P,0) (P-1,0) yuxarı qalxır. Bu qrupda f(P-1,Q) ümumi halların olduğunu bilirik, belə ki, nəticədə düzbucaqlı ölçü (P-1) x Q olacaq.
  - Buna görə də, hər mümkün yol bu iki qrupdan birinə düşəcəyindən, ümumi hallar sayı bu qrupların cəmidir. Bu, bizə eyni düsturu verir \(f(P,Q) = f(P,Q-1) + f(P-1,Q)\).
- Aşkar formulanın törəməsi
  - Sağ alt küncdən başlamaq əvəzinə, gəlin düzbucaqlını elə döndərək ki, nöqtə (P,0)-dan yuxarıda olsun. Artıq bunu aşağıdakı diaqramla vizuallaşdıra bilərik:
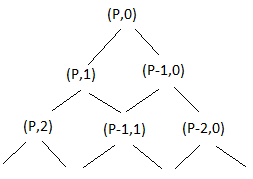
  - Bu tip diaqram ağac kimi tanınır. Biz (P,0) və ya (0,Q)-yə gedənə qədər bu nümunə təkrarlanacaq. Bu hadisə baş verəndə ağac lövhədən keçirə biləcəyi hər bir mümkün halı özündə ehtiva edəcək.
  - Bu ağacda yuxarıdan (P,1) düyünlərə (İ,J) çatma yollarının sayıdır. Daha sonra sağa enərək (İ,J), üstəlik,(İ,J-1) çatma yollarının sayı, sonra isə sola (İ,J) enmək. Başqa sözlə bu, Paskalın Üçbucağındakı ədəddir.
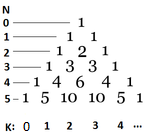
  - Paskal üçbucağında hər bir ədəd yuxarıdakı iki ədədin cəmidir. Sol sütundakı nömrələr boş lövhə ilə 0-dan başlayaraq lövhənin sıralarını sayır. Üçbucağın altındakı ədədlər həmçinin 0-dan başlayaraq soldan mövqeyi təmsil edir. K mövqeyindəki N'lər sırasındakı ədədə bərabərdir \({N \choose K} = \frac{N!}{(N-K)!K!}\).
  - f(p,q) rəqəminə rast gəlmək istəyirik. Bu ədədi (P,0) -dan (0,Q) əldə etmək üçün olan yollardır. Bunun üçün yuxarı P qədər sağa, Q qədər isə soldan aşağı enmək lazımdır. Daha əvvəl müəyyən etdiyimiz ağac quruluşundan istifadə edərək bu, (0,0) -dan (P,Q)-yə gəlmək ağacda yalnız sol və sağa getməklə eynidir.
  - Lakin bu, P+Q addımlarını düzəltməyimizə səbəb olur, buna görə də ağacda P+Q cərgəsindəyik. Q dəfə sağa hərəkət etdiyimizi bildiyimiz üçün Paskal Üçbucağında bu mövqedəki ədəd \({P+Q \choose Q} = \frac{(P+Q)!}{P!Q!}\).
- İnduksiya ilə açıq-aşkar düsturun isbatı
  - Aşağıdakı düsturların ekvivalent olduğunu göstərəcəyik. \[f(P,Q) = \begin{cases}1 & for & P=0 \\1 & for & Q=0 \\f(P,Q-1) + f(P-1,Q) & for & \text{P>0 and Q>0}\end{cases} = \Bigg\{{P+Q \choose Q} = \frac{(P+Q)!}{P!Q!}\]
  - İnduksiya Bazası: Biz artıq bilirik ki, f(0,0) = 1 düstur tərifi ilə. P=0 və Q=0-ı düsturda yerinə qoysaq, əldə edrik ki, \(\frac{(0+0)!}{0!0!} = \frac{0!}{1} = 1\). Bu, baza düsturların ekvivalent olduğunu göstərir ki, bu da induksiya bazasını bitirir.
  - İnduksiya Fərziyyəsi: Fərz edək ki, düsturlar P,Q-nün P+Q = N ilə bütün qiymətləri üçün ekvivalentdir.
  - İnduksiya addımı: İnduksiya fərziyyəsini istifadə edərək P,Q P+Q=N+1 ilə bütün dəyərlər üçün ekvivalentliyi sübut edirik. P+Q=N+1 ilə P,Q-nün hər hansı qiyməti üçün bizim 3 halımız var:
  - 1-ci məsələ:
  - 2-ci məsələ:
  - 3-cü məsələ: \(P,Q > 0\) \[ \begin{align} f(P,Q) &= f(P,Q-1) + f(P-1,Q)\qquad\qquad (+)\\ &= \frac{(P+Q-1)!}{P!(Q-1)!} + \frac{(P-1+Q)!}{(P-1)!Q!}\\ &= \frac{(P+Q-1)!Q}{P!(Q-1)!Q} + \frac{(P-1+Q)!P}{(P-1)!PQ!}\\ &= \frac{(P+Q-1)!}{P!Q!} (Q+P)\\ &= \frac{(P+Q)!}{P!Q!} \end{align} \]
  - (+): Əgər P + Q = N + 1 olarsa, onda P + Q-1 = N, yəni induksiya fərziyyəsi ilə.
    f(P,Q-1) = \(\frac{(P+(Q-1))!}{(P!(Q-1)!)}\), və eynilə f(P-1, Q) üçün
  - Bu, f(P,Q) üçün iki düsturun ekvivalent olduğunu göstərir.
  - İsbatların sonu. ∎

P sətir və Q sütunları neçə müxtəlif mövqelərə malikdirlər?
- P-1 sətirləri və Q-1 sütunları ilə düzbucaqlıya uyğun olan bütün mövqelər üçün sadəcə eyni düsturdan istifadə etmək olar. Bu da f(P-1,Q-1)-dir.

Daha çox qalib və ya daha çox uduzan mövqelər varmı?
- Əgər bir mövqedə N xana varsa, onda oyunçun 1 ilk gediş üçün N variantı var. İlk gedişi edə bilmək oyunçuya 1 üstünlük verir və bu, o deməkdir ki, uduzan mövqelərdən daha çox qalib mövqelər var. Daha əvvəlki bir əşyada 2,3,4 və ya 5 xanası olan mövqelər arasında neçə itki mövqeyi olduğu müəyyən edilmişdir. Burada bəzi ədədlər var ki, bu da mövqeyin nə qədər çox xanaya malik olduğunu təsdiqləyirsə, onun qələbə mövqeyi olma ehtimalı bir o qədər yüksəkdir.
- # xanalar # mövqelər # mövqelərini itirmək % mövqelərini itirmək
  20 627 42 6.69
  30 5604 220 3.92
  40 37338 1022 2.73
  50 204226 4976 2.43
  60 966467 20106 2.08
  70 4087968 76688 1.87
  80 15796476 270142 1.71
  90 56634173 897964 1.58
- 2 argument '# mövqelərin ' və '# itirilən mövqelərin' hansı funksiyası yuxarıdakı cədvəlin hər bir sətri üçün təqribən eyni dəyər verir?
  - Bu sualın cavabı aşağıdakı tapdığımız maddələrdə verilir.

# xanalar	# mövqelər	# mövqelərini itirmək	% mövqelərini itirmək
20	627	42	6.69
30	5604	220	3.92
40	37338	1022	2.73
50	204226	4976	2.43
60	966467	20106	2.08
70	4087968	76688	1.87
80	15796476	270142	1.71
90	56634173	897964	1.58

Caribou Fərziyyəsi

Bir qədər əvvəl biz göstərdik ki, hər bir mövqe ya qalib gələn, ya da uduzan mövqeyidir. Bu sübut bizə birbaşa metod verdi ki, onların uduzduğu və ya qalib gəldiyi bütün mövqelər üçün addım-addım müəyyən edək. Xüsusi olan odur ki, bu metodun heç bir axtarışa (hərəkətləri sınamağa) ehtiyacı yox idi. Bu, bütün sadə ədədləri müəyyən ölçülərə qədər müəyyən etmək üçün 'Sieve of Eratosthenes'ini xatırladırdı.

'Eratosthenes Sieve'haqqında oxuyun, məsələn, internetdə
- N² ölçüsünə qədər bütün sadə ədədləri tapmaq üçün, burada N tam ədəddir, aşağıdakıları etmək lazımdır:
- - A: P=2 sadə ədədi ilə başla.
  - B: N^2-yə qədər p-nin bütün çoxluqlarının üstündən xətt çək.
  - C: Hələ üstündən xətt çəkilməyən növbəti ən böyük ədədi > p tapın. Əgər bu ədəd > N olarsa, alqoritm dayanır. Əks halda, bu p ədədindən istifadə edin və B addımı ilə davam edin.
- N^2-yə qədər olan bütün ədədlər N² < hamısı sadı ədədlərdir. Bu alqoritmin geniş formasını tapa bilərsiniz https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes

Bu bənzərlik bizi sadə ədədlərlə mövqeləri itirmək arasında daha çox oxşarlıqlar düşünməyə ilham verdi. Bu, 'Sadə Ədəd Teoremi'nə bənzər mövqeləri itirməsi fərziyyəsinə gətirib çıxardı. Aşağıda detalları izah olunur.

Cədvəl: Chomp'da məğlub mövqe və sadə ədədlər arasındakı bənzərliklər:

Ədədlər	Chomp
Burada sonsuz sayda tam ədədlər var.	Burada sonsuz Chomp mövqeləri var.
Burada sadə və vuruqlarına ayrıla bilən ədədlər var.	Burada məğlub və qalib mövqelər var.
Burada sonsuz sayda sadə ədədlər var.	Burada sonsuz sayda məğlub mövqelər var.
Vuruqlarına ayrıla bilən ədəd sadə ədədlə ədədin hasilidir.	Qalib mövqe itirilən mövqe və mövqenin cəmidir (çünki hərəkətdə dayandırılan şey pilləkən şəklinə malikdir və buna görə də mövqedir).
Bir sadə ədəd məlum olduqdan sonra, bir nəfər dərhal bir çox vuruqlarına ayrıla bilən ədədi bilir (sadə ədədin bütün çoxluqları).	Bir itirilən mövqe məlum olduqdan sonra, bir nəfər dərhal bir çox qalibmövqeni bilir (bütün mövqelər, üst sətir və sol sütun boyunca sonsuz uzun olanlar da daxil olmaqla, künc düzbucaqlıları doldurmaq nəticəsində yaranır).
Böyük ədədin kiçik sadə ədədə bölünmə ehtimalı böyük sadə ədədə nisbətən daha yüksəkdir.	Böyük bir mövqe, böyük bir itirmə mövqeyinə nisbətən kiçik bir itki mövqeyinə görə daha çox azala bilər.
N ədədinin sadə ədəd olub-olmadığını müəyyən etmək üçün N-nin kvadrat kökünə qədər bütün sadə P ədədlərini bilmək çox səmərəlidir. Sonra N-nin P-yə bölünməsi ilə, yəni N-nin sınaq bölməsi ilə endirilə biləcəyini yoxlamaq olar N/ P.	P mövqeyinin məğlub mövqeyi olub-olmadığını müəyyən etmək üçün P-də olan bütün L mövqelərini bilmək lazımdır. Bundan sonra bir gedişlə P-nin L-ə endirilə biləcəyini effektiv şəkildə yoxlamaq olar.
'Sieve of Eratosthenes' bəzi N ədədinə qədər bütün sadə ədədləri təyin etmək, eyni zamanda verilmiş ədədin sadə ədəd olub-olmadığını yoxlamaq üçün effektiv üsuldur. Bu alqoritm yuxarıda təsvir edilmişdir.	'Sieve of Eratosthenes'ə bənzər bir şey {1} uduzma mövqeyi ilə başlayır və bir addımda bu uduzma mövqeyinə çatan bütün qalib mövqeləri aşır. Sonra oyunçu daha bir xana ilə bütün mövqeləri yoxlayır. Üzərindən xətt çəkilməyən bütün mövqelər itirilən mövqelərdir.
Sieve alqoritminin çatışmazlığı vuruqlarına ayrıla bilən ədədlərin üstündən təkrar-təkrar keçməkdir.	Sieve alqoritminin çatışmazlığı dəfələrlə qalib mövqelərin üstündən keçməkdir.
Əsas ədədlərin sıxlığı onların ölçüləri ilə azalır; i.e. nisbəti (# N tam ədədinə qədər sadə ədədlərin ) / N artdıqca, azalır.	Mövqelərini itirmə sıxlığı onların ölçüləri ilə azalır; i.e. nisbəti (# N xana qədər olan mövqeləri itirmək) / (# N xana ilə bütün mövqelərdən) N artdıqca azalır. (Sual: Bu nisbətin N-dən asılılığının düsuru nədir və bu, əsas ədədlərin sıxlığının düsturu ilə necə müqayisə olunur?).
Sadə ədəd teoremi: (# sadə ≤ N) / (N / log(N)) → 1 olaraq N → sonsuzluq.	Analoji fərziyyə: (#)N xanası ilə itirilən mövqelərin sayı) / ((#)N xanaları ilə mövqelərin / log (#)N xanaları ilə mövqelərin #)) → 0,283... N → sonsuzluq kimi.

Cədvəl: Chomp'da məğlub mövqe və sadə ədədlər arasındakı fərqlər:

Ədədlər	Chomp
Bütün tam ədədlərin çoxluğu tam nizamlanmış çoxluqdur; yəni istənilən iki ədəd arasında hansının daha böyük olduğunu bilinir.	Bütün Chomp mövqelərinin sırası qismən sıralanmış çoxluqdur. Mövqelər tamamilə başqa mövqelərdə saxlanıla bilər, lakin buna ehtiyac yoxdur.
Bir ədədi öz sadə vuruqlarına ayırmaq əməliyyatı bölünmədir.	Bir mövqenin itirilən mövqeyə çevrilməsi əməliyyatı xanaların çıxılmasıdır.
Bir ədədi bir ölçülü ədəd oxunda sətir seqmenti kimi vizuallaşdırmaq olar.	Mövqe ölçülərinə görə sıralanmış ədədlərin siyahısı vasitəsilə müəyyən edilir və beləliklə, 2D obyektdir.

Açıq Suallar:

Fərziyyə (# N xana ilə mövqeləri itirmək) / (# N xana ilə mövqelər) / log(# N xana ilə mövqeləri itirmək)) → 0.283... N → sonsuzluq doğru olduğu kimi?

İsbat edə bilərsinizmi? (Hələ ki, bacarmırıq :-) )

Chomp'un Müxtəlif Versiyaları

Yuxarıda oynanılmış Chomp oyunu 2D Chomp versiyasıdır. Bu o deməkdir ki, lövhə eni və hündürlüyü ilə cəmi 2 ölçülüdür.

3D Chomp versiyasını təsəvvür edə bilərsinizmi?
- Oyuna yeni ölçü əlavə etməyi təsəvvür etməyin ən sadə yolu lövhəyə üçüncü ölçü əlavə etməkdir. Yeni lövhənin sadəcə eni və hündürlüyü əvəzinə uzunluğu, eni və hündürlüyü olacaqd. Əgər biri ilə oynamaq üçün kublar az olsaydı, məsələn, zər, onlar aşağıdakı şəkildə göstərildiyi kimi bu 3D oyunu oynaya bilərdilər.
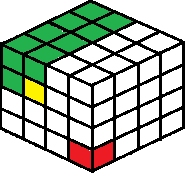
- Bir hərəkət edərkən, seçilən kubu, eləcə də hər bir seçilmiş kubun solunda, yuxarısında və yuxarı hissəsindəki hər bir kubu aradan qaldırardılar. Görüntüdə nümunəvi gediş sarı rəngdə vurğulanır. Bu hərəkət həmçinin görüntüdəki bütün yaşıl xanaları da aradan qaldırır. Şəkildəki qırmızı xananın göstərdiyi son xananı götürən şəxs oyunu itirən oyunçudur.
- Həqiqi kublarla oyunu asanlaşdırmaq üçün kubları küncə, məsələn, ayaqqabı qutusunun küncünə itələmək olar ki, qırmızı xana qutunun ən küncündə olsun və bütün digər kublar yalnız bir dəfə əlçatan olsun. Qutudan istifadə etmək lazım deyil, amma bu, kubları sabitləşdirir və bütün quruluşu pozmadan kubu aradan qaldırmağı asanlaşdırır.

Daha çox ölçüdə Chomp oynamaq haqqında nə demək olar?
- Daha əvvəl müəyyən etdik ki, Chomp oyununa yeni ölçü əlavə etmək kifayət qədər asandır. Əgər biri Chomp'u 3D-dən daha yüksək ölçüdə oynamaq istəsəydi, Chomp lövhəsinə yeni ölçülər əlavə etməyə davam edərdi. Lakin 3D-dən sonra artıq bloklardan istifadə edərək Chomp lövhəsini genişləndirmək mümkün deyil. Bununla belə, karandaş və kağızdan istifadə edərək Chomp oyununu genişləndirmək etmək üçün bir yol var. Bu üsul bizə oyunu yalnız 2D və ya 3D deyil, istənilən sayda ölçülərdə oynamağa imkan verir.
- Kağız üzərində 2D Chomp oyunu oynamaqla başlayacağıq. Oyunda bunu tətbiq etmək üçün bir yol ilk əvvəl yalnız 2 müxtəlif əsas vuruğu olan bir ədəd seçməkdir. Məsələn, 72 = 2^{3 x 3} ². Sonra bu ədədin bütün vuruqlarını aşağıda göstərildiyi kimi düzbucaqlı şəklində yazırıq.
- 72 36 18 9
  24 12 6 3
  8 4 2 1
- İstənilən sağ qonşu rəqəm 2 vuruqla daha kiçik, altında isə hər hansı qonşu rəqəm 3 vuruqla daha kiçikdir. Bu lövhədə hərəkət etmək üçün ədəd seçmək lazımdır. Sonra həmin ədədin vuruqlarından hər hansı biri ilə birlikdə onu aradan qaldırardınız. Kim 72 rəqəmini götürürsə, oyunu uduzur.
- Daha böyük ilkin düzbucaqlıya malik olmaq üçün 2^P x 3^Q düsturundan istifadə etməklə daha böyük ədəd tapmaq olar. P və Q-nü daha böyük ədədlərlə əvəz etməklə 2D-də Chomp üçün daha böyük lövhələr əldə etmək olardı.
- Yüksək Ölçü üçün Bu Simulyasiyanı Necə Bir Daha Ümumiləşdirə bilərsiniz?
  - Chomp' un karandaş və kağız versiyasını 2D-dən 3D-yə qədər genişləndirmək üçün sadəcə başlanğıc sayını tapmaq üçün istifadə olunan düsturu genişləndirmək lazımdır. Bəlkə, 2 fərqli sadə vuruğa malik olan ədədi seçmək əvəzinə, kimsə 3 fərqli sadə vuruğa malik olan ədədi seçir. Bu ədədi tapmaq üçün yeni düsturdan istifadə edə bilərik: 2^P x 3^Q x 5^R. Sonra, əvvəlki kimi eyni üsullardan istifadə edərək, oyun 3 ölçüdə simulyasiya edilə bilər. Hətta daha böyük ölçülər əldə etmək istədiyinizdə ölçülərin sayından asılı olaraq sadəcə olaraq düstura yeni sadə ədədləri əlavə etmək kifayətdir.

İstinadlar